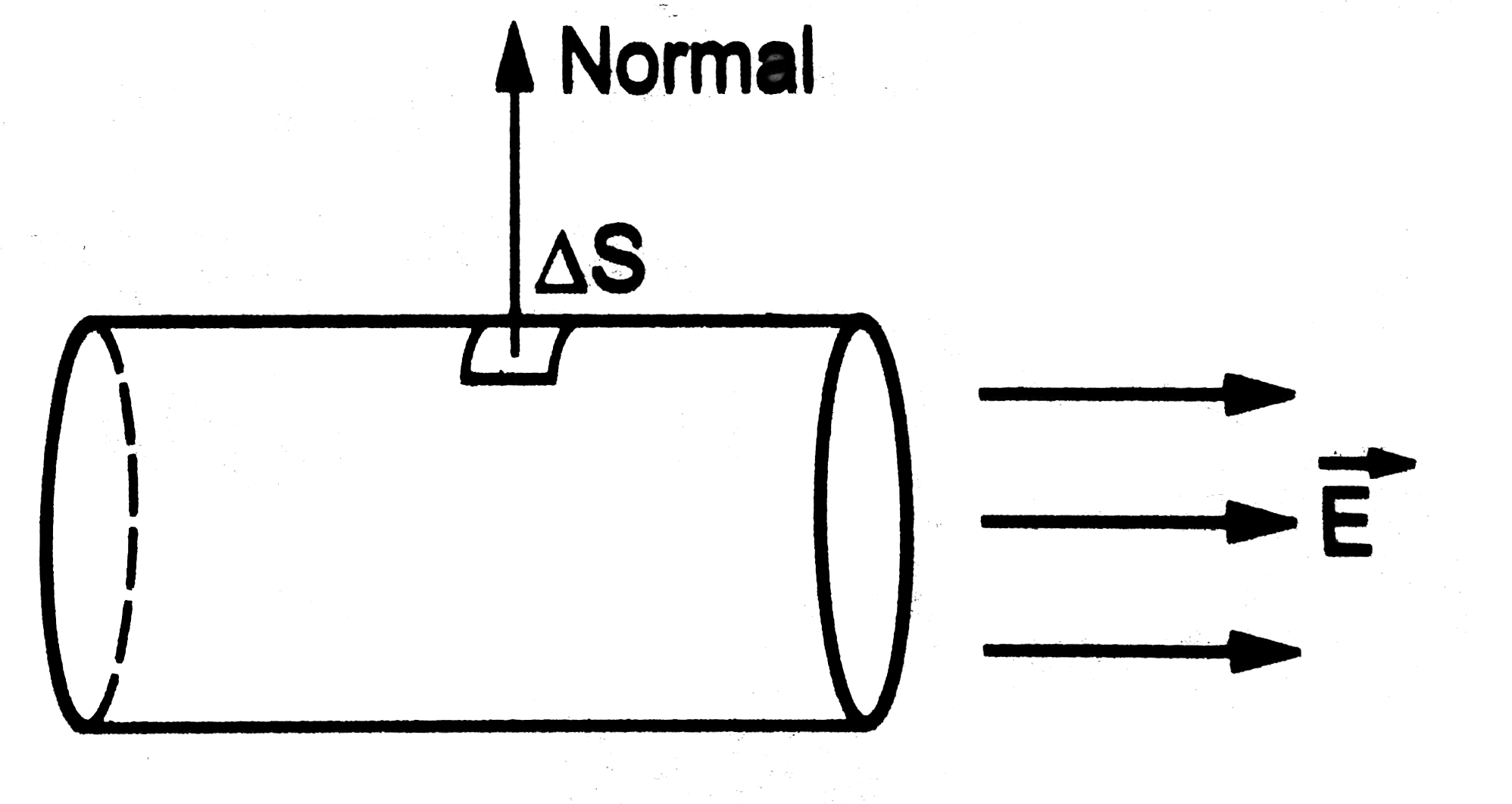
A uniform electric field exists in space. Find the flux of this field through a cylindrical surface with the axis parallel to the field.Solution in Gujrati
Consider figure and take a small area ΔS on the cylinderical surface. The normal to this area will be perpendicular to the axis of the cylinder. But the electric field is parallel t o the axis and henc
ΔΦ=→E⋅→S=EΔ→S=EΔScos(π/2)=0
This is true for each small part of the cylinderical surface. Summing over the entire surface. the total flux is zero.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - GAUSS LAWEXERCISE - Worked Out Examples8videos
GAUSS LAW
- BOOK - HC VERMACHAPTER - GAUSS LAWEXERCISE - Short Answer7videos
GAUSS LAW
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises9videos
ELECTROMAGNETIC WAVES
- BOOK - HC VERMACHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercises77videos
GEOMETRICAL OPTICS
Similar Questions
A uniform electric field of magnitude E=100NC−1 exists in the space in x-direction. Calculate the flux of this field through a plane square of edga 10 cm placed in the y-z plane. Take the normal along the positive x-axis to be positive.
03:45View SolutionA small plane area is rotated in an electric field. In which orientation of the area is the flux of electric field through the area maximum? In which orientation is it zero.?
04:09View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
02:32View SolutionA concave mirror having a radius of curvature 40 cm is placed in front of an illuminated point source at a distance of 30 cm from it. Find the location of the image.
02:18View SolutionA uniform electric field exists in space. Find the flux of this field through a cylindrical surface with the axis parallel to the field.
02:35View SolutionConsider a cylindrical surface of radius R and length l in a uniform electric field E. Compute the electric flux if the axis of the cylinder is parallel to the field direction.
View SolutionA hollow half cylinder surface of radius R and length l is placed in a uniform electric field vecE . Electric field is acting perpendicular on the plane ABCD. Find the flux through the curved surface of the hollow cylindrical surface
02:06View SolutionA cyclinder of radius r and length l is placed in an uniform electric field in such a way that the axis of the cyclinder is parallel to the field. The flux of the field through the cyclindrical surface is
02:58View SolutionA uniform electric field exists in space. Find the electric flux of the filed thourgh curved surface area of the cyclinder with its axis paralel to the field.
02:15View SolutionA Gaussian surface in the cylinder of cross-section pia^(2) and length L is immersed in a uniform electric field E with the cylinder axis parallel to the field. The flux phi of the electric field through the closed surface is
03:21View Solutionयदि पृष्ठ विद्युत क्षेत्र के समांतर है तो उससे गुजरने वाले विद्युत फ्लक्स का मान शून्य होता है।
02:11View SolutionThe electric flux through a hemispherical surface of radius R placed in a uniform electric field E parallel to the axis of the circular plane is
04:29View SolutionA uniform field E is parallel to axis of a hollow hemisphere of radius - Ε Axis Electric flux through the hemispherical surface is
04:38View SolutionA uniform electric field exists in space. Find the flux of this field through a cylindrical surface with the axis parallel to the field.
02:43View SolutionA Gaussian surface in the cylinder of cross-section πa2 and length L is immersed in a uniform electric field E with the cylinder axis parallel to the field. The flux ϕ of the electric field through the closed surface is
05:24View SolutionExplain the concept of electric field. Express electric flux through a surface in terms of electric field cylindrical surface with its axis parallel to uniform electric field is zero,
03:18View Solution

