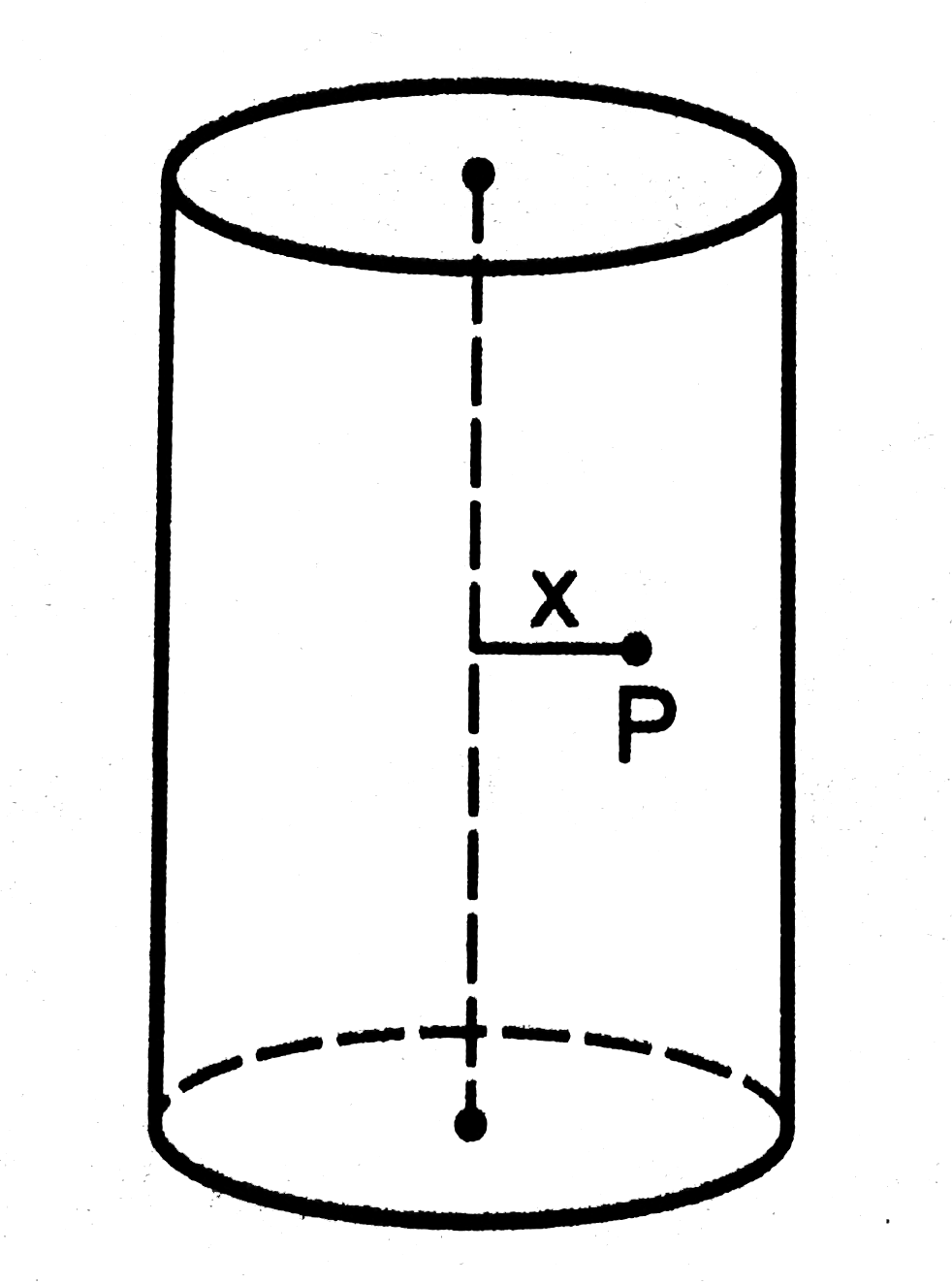
A long cylindrical volume contains a uniformly distributed charge of dendity ρ. Find the electric field at a point P inside the cylindrical volume at a distance x from its axis (figure 30-E5) ,
 Solution in Gujrati
Solution in Gujrati
Charge on the cylinder of radius x
=ρπ(x2)h
We know,
∮E.ds=qε0
E.2πxh=(πρ(x2)hε0)<br>orE= rhox / 2 epsilon_0.
Topper's Solved these Questions
Similar Questions
Mark the correct option:
05:58View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
03:29View SolutionA concave mirror having a radius of curvature 40 cm is placed in front of an illuminated point source at a distance of 30 cm from it. Find the location of the image.
04:25View SolutionA ring of radius a contains a charge q distributed uniformly over its length. Find the electric field at a point on the axis of the ring at a distance x from the centre.
02:09View SolutionA long cylindrical volume contains a uniformly distributed charge of dendity ρ. Find the electric field at a point P inside the cylindrical volume at a distance x from its axis (figure 30-E5) ,
 View Solution
View SolutionA long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
04:15View SolutionAn polaroid long cylindrical object with radius R has a charge distribution that depends upon distance r from the axis like this : rho = ar + br^(2)(r le R , a and b are non zero constant, rho is volume charge density). If electric field outside the cylinder is zero than value of (a)/(b) is :
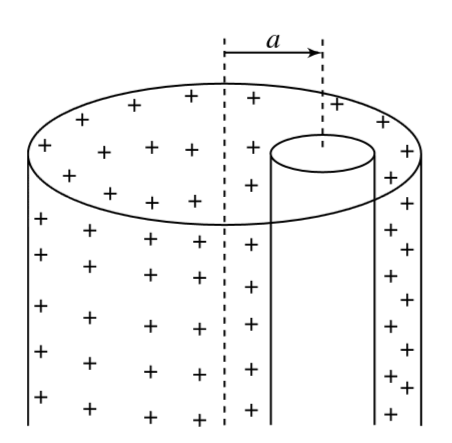
05:35View Solution(a) There is a long uniformly charged cylinder having a volume charge density of ρC/m3. Radius of the cylinder is R. Find the electric field at a point at a distance x from the axis of the cylinder for following cases (i) x lt R (ii) x gt R What is the maximum field produced by the charge distribution at any point? (b) The cylinder described in (a) has a long cylindrical cavity. The axis of cylindrical cavity is at a distance a from the axis of the charged cylinder (see figure). Find electric field inside the cavity.
 02:26View Solution
02:26View SolutionA long cylindrical volume (of radius R) contains a uniformly distributed charge of density rho . Consider a point P inside the cylindrical volume at a distance x from its axis as shown in the figure. Here x can be more than or less than R. Electric field at point P is :
02:17View SolutionA ring of radius a contains a charge q distributed. uniformly ober its length. Find the electric field at a point. on the axis of the ring at a distance x from the centre.
View SolutionA long cylindrical volume contains a uniformly distributed charge of density ρ. Find the electric field at a point P inside the cylindrical volume at a distance x from its axis (figure 30-E5) ,
 View Solution
View SolutionA long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
09:29View SolutionInside an infinitely long circular cylinder charged uniformly with volume density P ther is a circular cylindrical cavity. The distance between the axis of the cylinder and the cavity is equal to a. Find the electric field strenght E inside the cavity. The permittivity us assumed to be equal to unity.
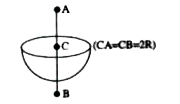
View SolutionThe diagram shows a uniformly charged bemisphere of radius R. It has volume charge density ρ. If the electric field at a point 2R distance below its centre ?
 02:31View Solution
02:31View SolutionFind the electric field at an arbitrary point of a sphere carrying a charge uniformly distributed over its volume.
03:47View SolutionFind the electric field at an arbitrary point of a sphere carrying a charge uniformly distributed over its volume.
04:14View Solution

