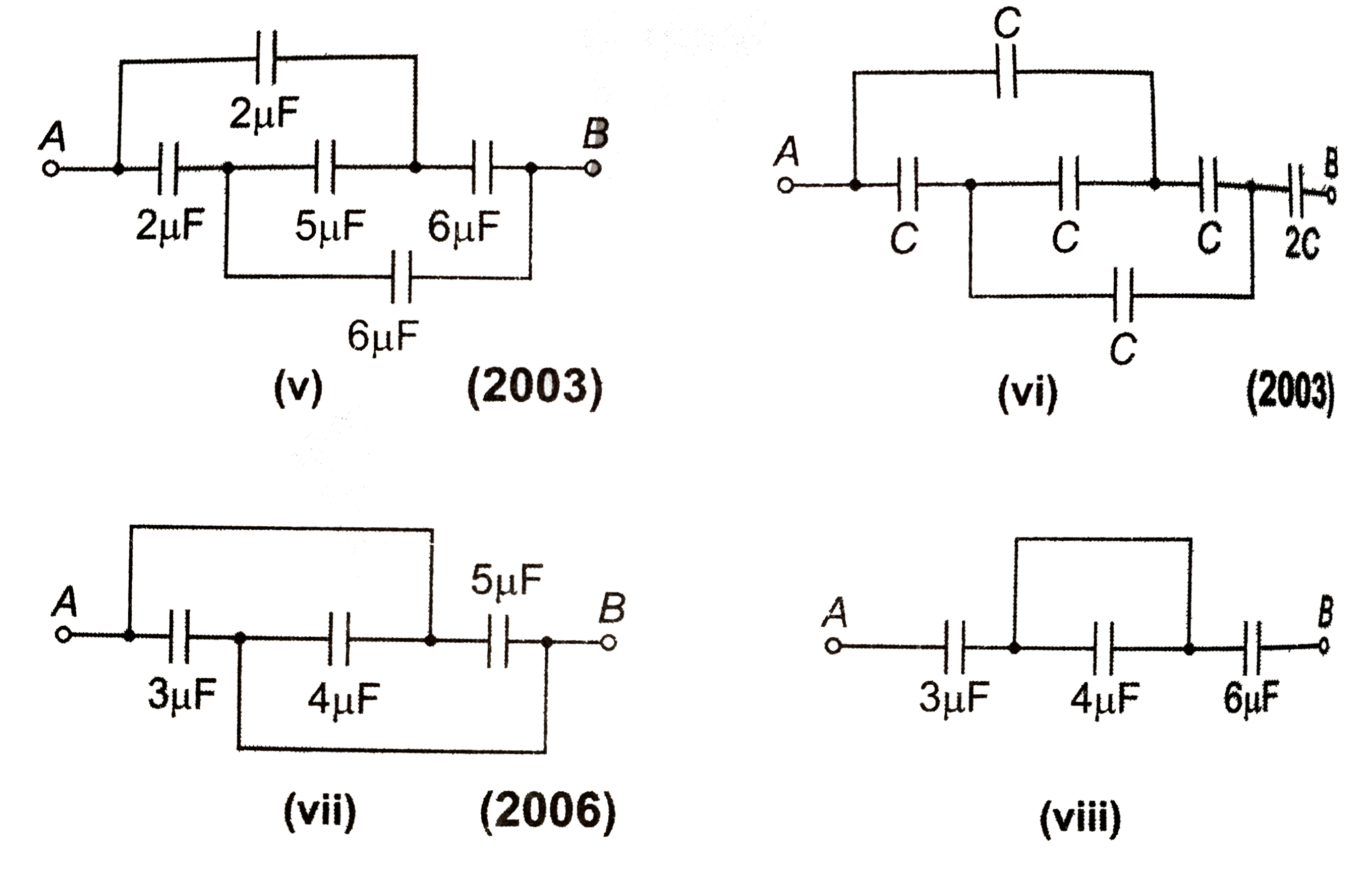
Find the equivalent capacitance between the point A and B in figure .
 Solution in Gujrati
Solution in Gujrati
Let us connect a battery between the points A and B. The charge distribution is shown jin figure. Suppose the positive terminal of the battery supplies a charge +Q and the negative terminal a charge -Q. The charge Q is divided between plates a can e. A charge <br>Q_1<br> goes to the plate a and the rest <br>Q-Q_1<br> goes to the plate e. The charge -Q supplied by the nagative terminal is divided between plates d and h. Using the symmetry of the figure, charge <br>-Q_1<br> goes to the plate h and <br>-(Q - Q_1)<br> to the plate d. This is because if you look into the circuit from A or from B, the circuit looks identical. The division of charge at A and at B should, therfore, be similar. The charges on the other plates may be written easily. The charge on the plate l is <br>2 Q_1 - Q<br> which ensures that the total charge on plates b,c and i remains zero as these three plates form an isolated system. we have <br>V_A V_B =(V_A - V_D) + (V_D - V_B)<br> = <br>(Q_1)/(C_1) + (Q- Q_1)/(C_2)<br> ... (i) Also, <br>V_A - V_B = (V_A - V_D) + (V_D - V_E) + (V_E - V_B)<br> = (Q_1)/(C_1) + (2Q_1 - Q)/(C_3) = (Q_1)/(C_1)<br>. ....(ii) We have to eliminate <br>Q_1<br> from these equations ot get the equivalent capacitance <br>Q/ (V_A- V_B)<br>. The first equation may be written as <br>V_A - V_B = Q_1 ((1)/(C_1) - (1)/(C_2)) + (Q)/(C_2)<br> or, <br>(C_1 C_2)/(C_2 - C_1) (V_A - V_B ) = Q_1 + (C_1)/(C_2 - C_1) Q<br>. The second equation may be written as <br> V_A - V_B = 2Q_1((1)/(C_1)+(1)/(C_3)) - (Q)/(C_3) or, (C_1 C_3)/(2(C1 + C_3) (V_A - V_B) = Q_1 - (C_1)/(2(C_1 + C_3) Q. ...(IV) Subtracting (iv) from (iii) <br>(V_A - V_B)[(C_1 C_2)/(C_2 - C_1) - (C_1 C_3) /(2(C_1 + C_3))]<br> <br> = [(C_1)/(C_2 -C_1) +(C_1)/(2(C_1 + C_3)] Q<br> or <br>(V_A - V_B) [2 C_1 C_2(C_1 + C_3) + (C_2 - C_1)]<br> <br>=C_1[2(C_1 + C_3) + (C_2 - C_1)] Q<br> or, <br> C = (Q)/(V_A - V_B) = (2 C_1 C_2 + C_2 C_3 + C_3 C_1)/( C_1 + C_2 + 2C_3)<br>.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - CAPACITORSEXERCISE - Short Answer7videos
CAPACITORS
- BOOK - HC VERMACHAPTER - CAPACITORSEXERCISE - Objective 112videos
CAPACITORS
- BOOK - HC VERMACHAPTER - CAPACITORSEXERCISE - Exercise2videos
CAPACITORS
- BOOK - HC VERMACHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Exercises46videos
BOHR'S MODEL AND PHYSICS OF THE ATOM
- BOOK - HC VERMACHAPTER - DISPERSION AND SPECTRAEXERCISE - Exercises11videos
DISPERSION AND SPECTRA
Similar Questions
Suppose a charge +Q1 is given to the positive plates and a charge −Q2 to the negative plate of a capacitor. What is the "charge on the capacitor"?
02:50View SolutionA capacitor of capacitance C is charged to a potential V. The flux of the electric field through a closed surface enclosing the capacitor is
09:54View SolutionThe plates of a paraller-plate capacitor are made of circular discs of radii5.0cm each .If the separation between the plates is 1.0mm,What is the capacitance?
02:18View SolutionThe bohrradius is given by a0=ε0h2πme2 verify that the RHS has dimesions of length
04:48View SolutionA flint glass prism and a crown glass prism are to be combined in such a way that the deviation of the mean ray is zero. The refractive index of flint and crown glasses for the mean ray are 1.620 and 1.518 respectively. If the refracting angle of the flint prism is 6.0∘, what would be the refracting angle of the crown prism ?
02:56View SolutionFind the equivalent capacitance of the system shown in figure between the points a and b.
 01:43View Solution
01:43View SolutionFind the equivalent capacitance between the point A and B in figure .
 03:02View Solution
03:02View SolutionAll the capacitances shown in figure are in muF . Find the equivalent capacitance between A and B.
04:28View SolutionFind the equivalent capacitance of the infinite ladder shown in figure between the points A & B .
03:47View Solution
Find the equivalent capacitance of the combination shown in figure. Between the points A and B.11:06View Solution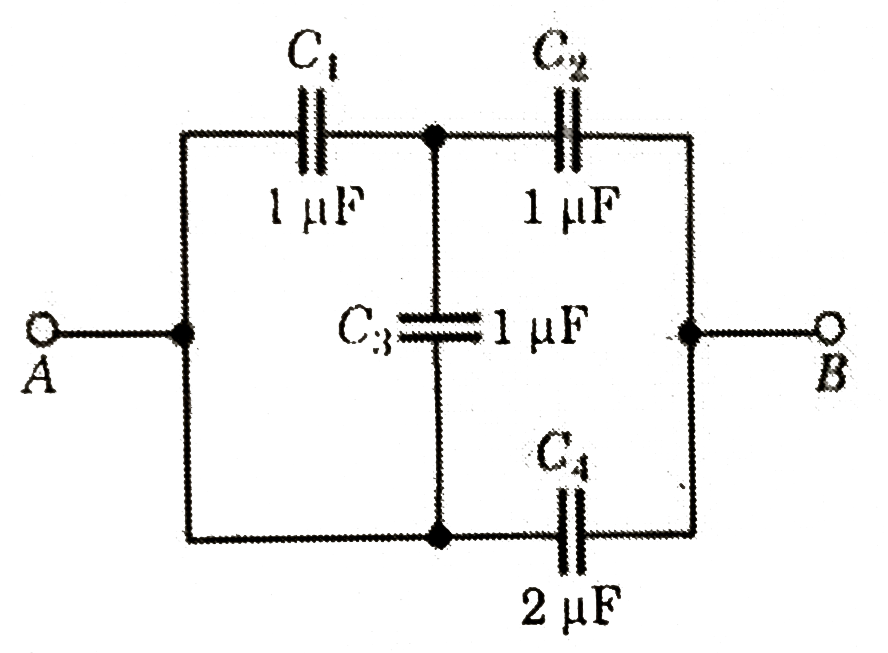
Find the equivalent capacitance between points A and B for the network shown in figure.03:01View Solutionचित्र में, बिंदु A व B के बीच तुल्य धारिता ज्ञात कीजिये।
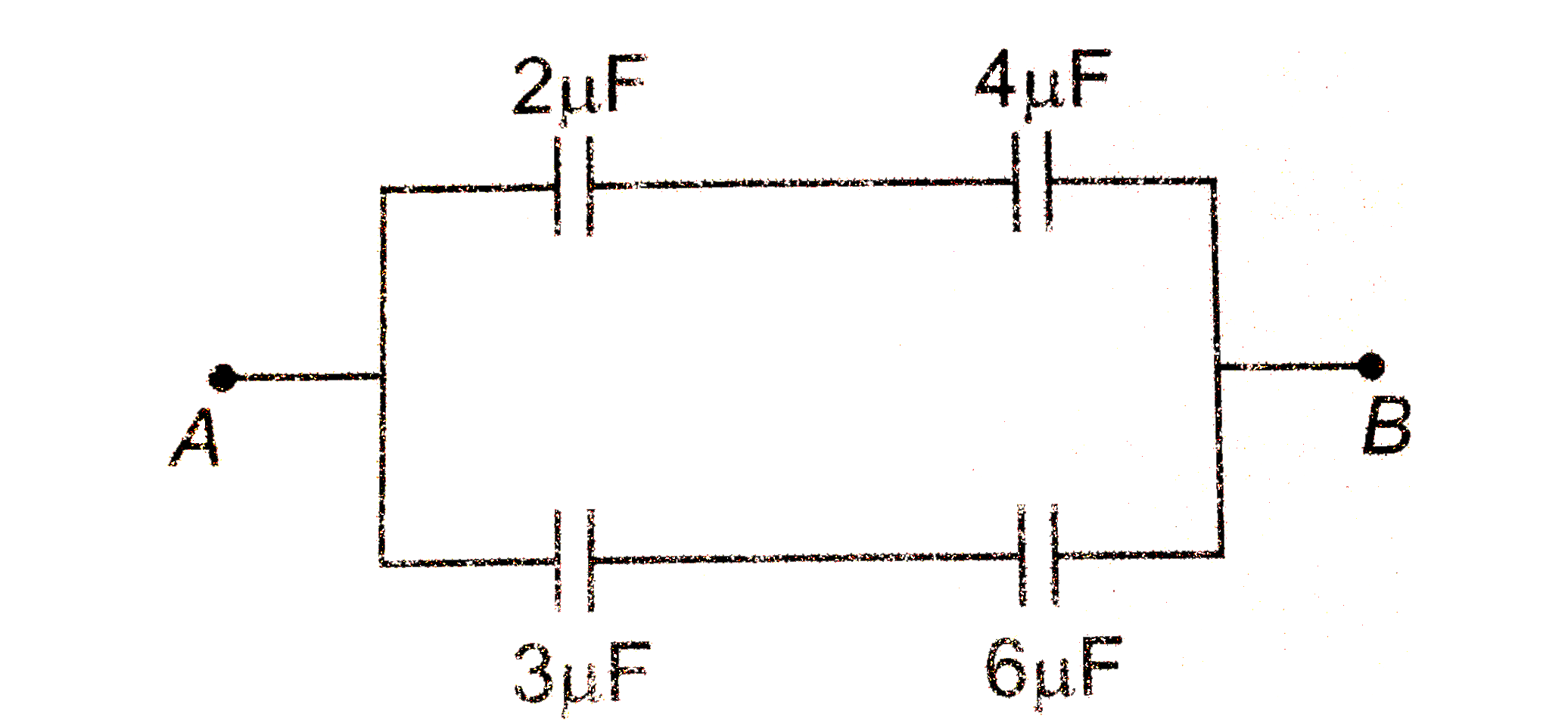 03:06View Solution
03:06View Solutionचित्र a,b तथा c में बिंदु P तथा Q के बीच तुल्य धारिता ज्ञात कीजिये।
 02:21View Solution
02:21View Solutionसंलग्न चित्र a में दिए गए परिपथ में A or B बिंदुओं के बीच तुल्य धारिता ज्ञात कीजिये।
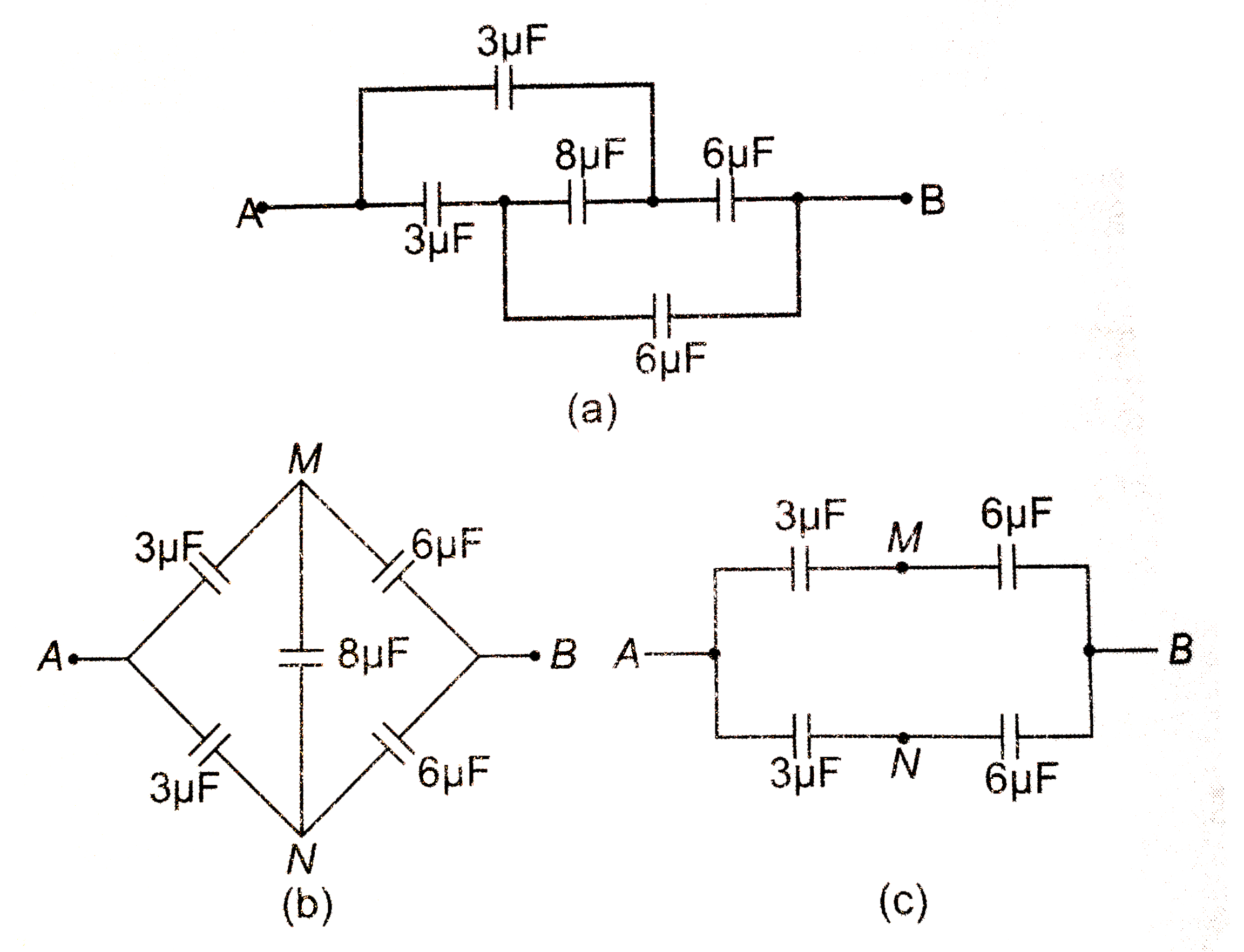 02:22View Solution
02:22View Solutionनिम्न चित्र में बंदु A or B के बीच तुल्य धारिता ज्ञात कीजिये।
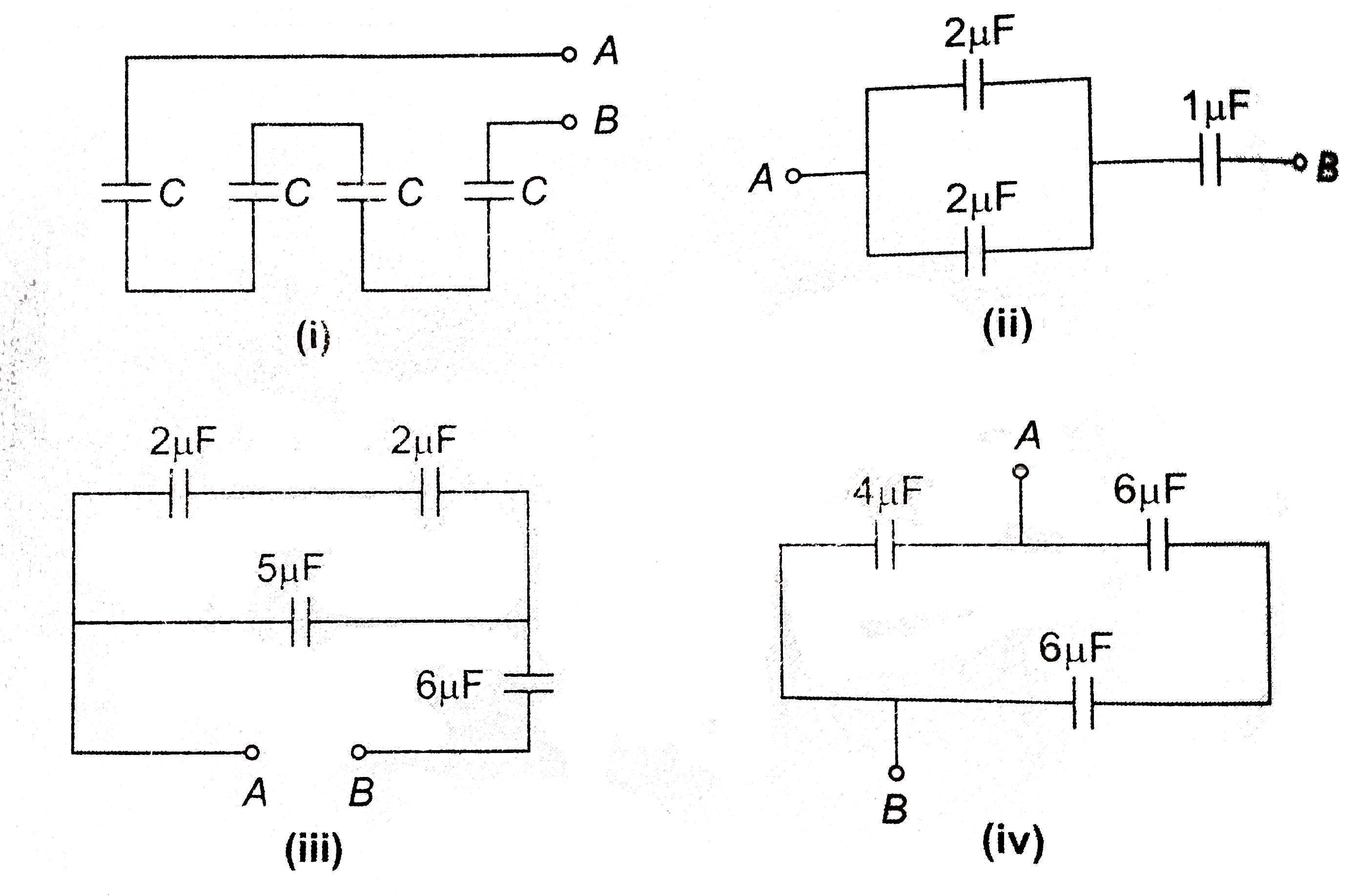
 02:02View Solution
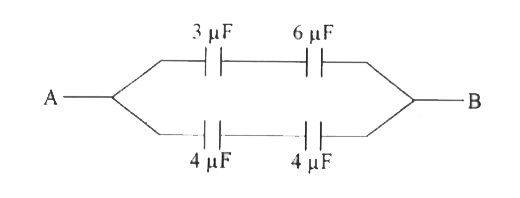
02:02View Solutionदिए गए चित्र में बिंदु A तथा B के मध्य तुल्य धारिता का मान होगा---
 03:56View Solution
03:56View Solution
