Twelve capacitors, each having a capacitance C, are connected to form a cube. Find the equivalent capacitance between the diagonally opposite corners such as A and B.
 Solution in Gujrati
Solution in Gujrati
Suppose the points A and B are connected to a battery. The charge appearing on some of the capacitors are shown in figure. Suppose the positive termainal of the battery supplies a charge is divided on the three plates connected to A. Looking from A, the three sides of the cube have identical properties and hence, the charge will be eually distributed on the three plates. Each of the capacitors a, b and c will receive a charge Q/3. The nagative terminal of the battery supplies a charge - Q through the point B. This is again divided equally on the three plates connected to B. Each of hte capacitors d, e and f gets equal charge Q/3. Now consider the capacitors g and h. As the three plates connected to the point E form and isolated system, their total charge must be zero. the nagative plate of g and h connected to E should have a total charge Q/3. By symmetry, these two plates should have equal charges and hence each of these has a charge Q/6. The capacitors a, g and d have charges Q/3, Q/6 and Q/3 respectively. we have, <br> V_A - V_B = (V_A - V_E) + (V_E - V_F) + (V_F - V_B)<br> <br>= (Q/3)/(C ) +(Q/6)/(C ) + (Q/3)/(C) = (5Q)/(6C)<br>. or, <br>C_(eq) = (Q)/(V_A - V_B) = (5)/(6) C.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - CAPACITORSEXERCISE - Short Answer7videos
CAPACITORS
- BOOK - HC VERMACHAPTER - CAPACITORSEXERCISE - Objective 112videos
CAPACITORS
- BOOK - HC VERMACHAPTER - CAPACITORSEXERCISE - Exercise2videos
CAPACITORS
- BOOK - HC VERMACHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Exercises46videos
BOHR'S MODEL AND PHYSICS OF THE ATOM
- BOOK - HC VERMACHAPTER - DISPERSION AND SPECTRAEXERCISE - Exercises11videos
DISPERSION AND SPECTRA
Similar Questions
Suppose a charge +Q1 is given to the positive plates and a charge −Q2 to the negative plate of a capacitor. What is the "charge on the capacitor"?
04:00View SolutionA capacitor of capacitance C is charged to a potential V. The flux of the electric field through a closed surface enclosing the capacitor is
06:55View SolutionThe plates of a paraller-plate capacitor are made of circular discs of radii5.0cm each .If the separation between the plates is 1.0mm,What is the capacitance?
View SolutionThe bohrradius is given by a0=ε0h2πme2 verify that the RHS has dimesions of length
05:37View SolutionA flint glass prism and a crown glass prism are to be combined in such a way that the deviation of the mean ray is zero. The refractive index of flint and crown glasses for the mean ray are 1.620 and 1.518 respectively. If the refracting angle of the flint prism is 6.0∘, what would be the refracting angle of the crown prism ?
05:52View SolutionTwelve capacitors, each having a capacitance C, are connected to form a cube . Find the equivalent capacitance between the diagonally opposite corners such as A and B.
 08:22View Solution
08:22View SolutionFind the equivalent capacitance between A and B. All the capacitors have capacitance C.
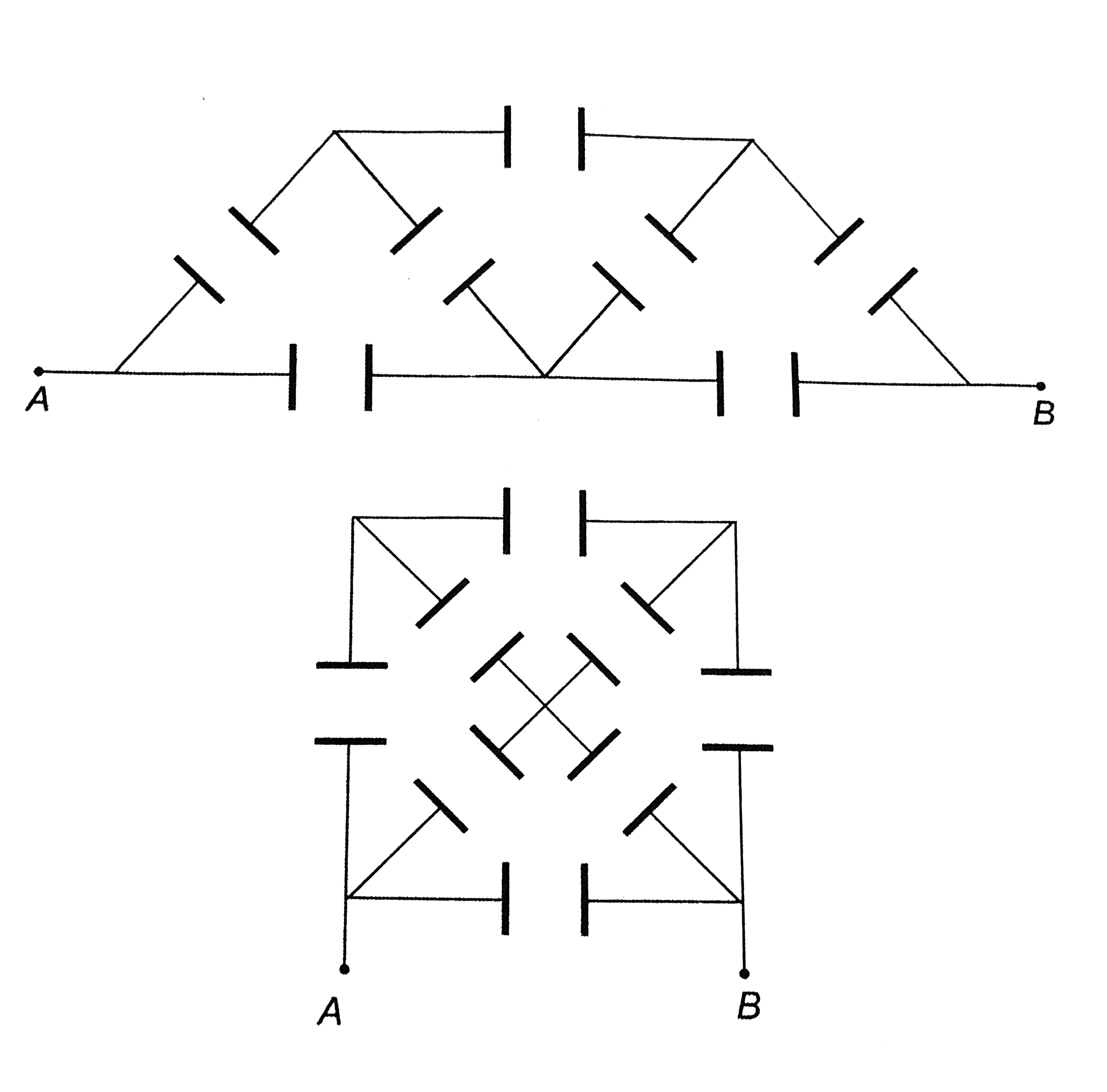 04:24View Solution
04:24View SolutionTwelve capacitors, each having capacitors, C , are joined to from a cube as shown. Find the equivalent capacitance between the ends of (a) Digitonal i.e., between A and B . (b) Face diagonal i.e., between A and C . (c) side of cube i.e., between A and D .
09:56View SolutionFind the equivalent capacitance between terminals A & C , if each capacitor is of capacitance 4muF
View SolutionTwelve wires, each of resistance 6Ω are connected to form a cube. The effective resistance between two diagonally opposite corners of the cube is
07:39View SolutionIf each capacitor has capacitance C, then equivalent capacitance between A and B is
05:58View Solutionचित्र में प्रत्येक संधारित्र की धारिता 1μF है। A व B के मध्य तुल्य धारिता ज्ञात कीजिये।
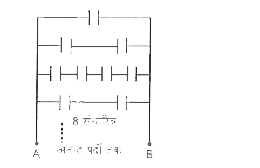 04:03View Solution
04:03View SolutionFind the equivalent capacitance between points A and B. Capacitance of each capacitor is 2muF .
View SolutionFigure shows a combination of twelve capacitors each of capacitance C forming a cube . Find the equivalent capacitance of the combination ( a) between the diagonally opposite corners A and B of cube ( b) between the diagonally opposite corners A and D of a face of the cube .
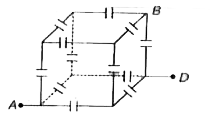 03:59View Solution
03:59View SolutionTwelve identical capacitors of capacitance C are connected across each edge of a cube. Find equivalent capacitance across one of the edges.
04:10View SolutionTwelve identical capacitors of capacitance C are connected across each edge of a cube. Find equivalent capacitance across one of the face diagonals.
03:59View Solution
