Question

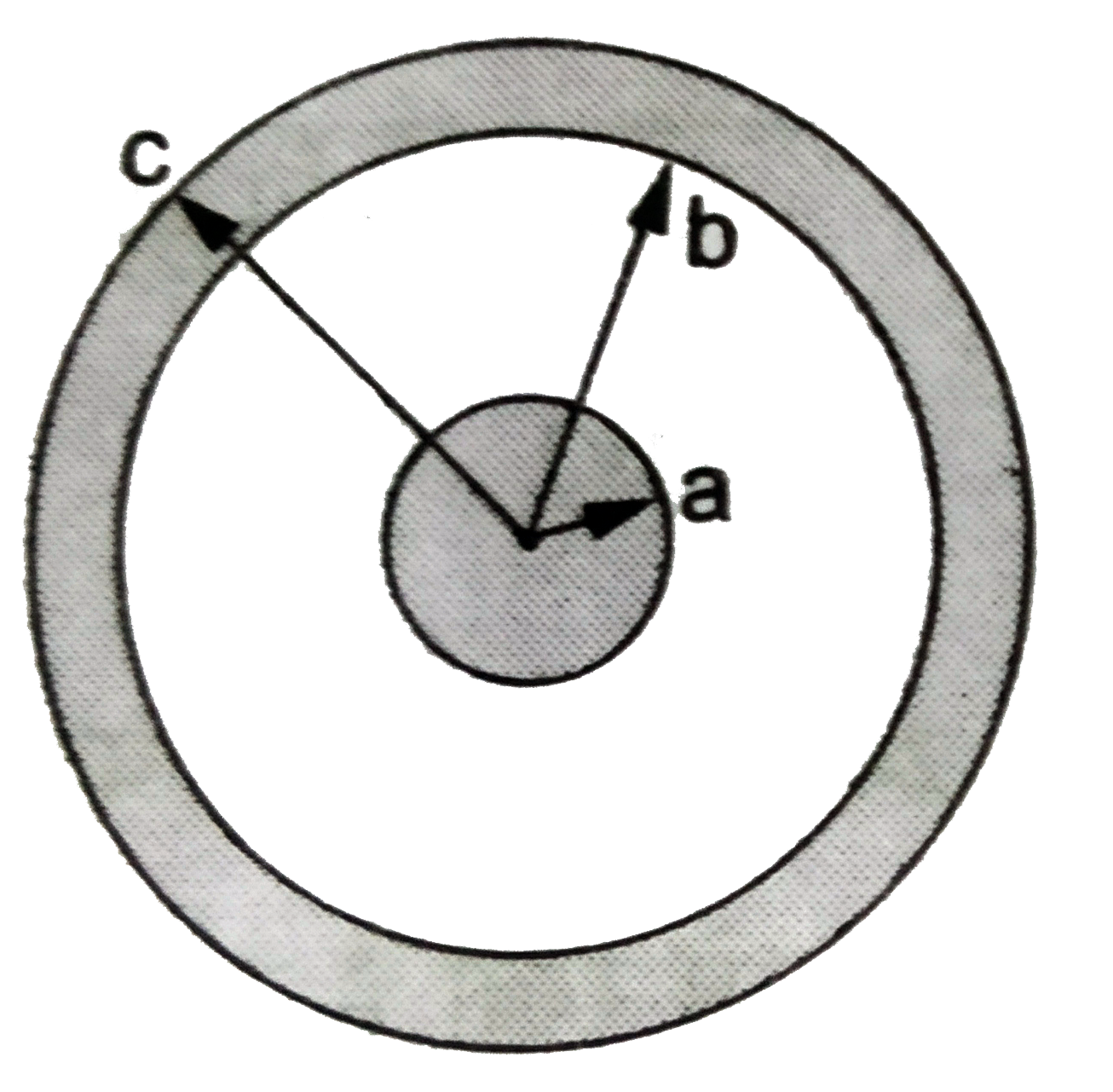
Consider a coaxial cable which consists of an inner wire of radius a surrounded by an outer shell of inner and outer radii b and c respectively. The inner wire carries an electric current (i_0) and the outer shell carries an equal current in opposite direction. Find the magnetic field at a distance x from the axis where (a) xlta, (b) altxltb, (c) bltxltc and (d)xgtc. Assume that the current density is uniform in the inner wire and also uniform in the outer shell.

Explanation

Solution: A cross section of the cable is shown in figure.
Draw a circle of radius x with the centre at the axis of
the cable. The parts a,b,c and d of the figure
correspond to the four parts of the problem.By
symmetry, the magnetic field at each point of a circle
will have the same magnitude and will be tangential to
it. The circulation of B along this circle is, therefore,
` oint (vec B). vec dl = B 2 pi x `
in each of the four parts of the figure.
` (a) The current enclosed within the circle in part a is `
` (i_0)/((pi a)^2). pi x^2 = ((i_0/a^2)x^2).`
` Ampere's law oint (vec B). (vec dl)= (mu_0)i gives `
` B 2 pi x = ((m_0)(i_0)(x^3)/(a^2)) or B= (((mu_0)(i_0)x)/((2 pi a)^2))`
The area of cross section of the outer shell is
` pi c^2- pi b^2. The area of cross section of the outer shell`
` within the circle in part c of the figure is (pi x^2 - pi b^2). `
` Thus, the current through this part is ((i_0(x^2-b^2))/(c^2-b^2)). This is`
` in the opposite direction to the current (i_0) in the inner `
` wire. Thus, the net current enclosed by the circle is `
` (i_0)-((i_0(x^2-b^2))/(c^2-b^2))= ((i_0(c^2- x^2))/(c^2-b^2))` .
From Ampere's law,
` B 2pix= ((mu_0)(i_0)(c^2-x^2)/(c^2-b^2))`
` or, B= ((mu_0)(i_0)(c^2-x^2)/(2 pi x (c^2-b^2))).`
` (d) The net current enclosed by the circle in part d of `
the figure is zero and hence
` B 2pi x = 0 or, B=0.`