In a coaxial, straight cable, the central conductor and the outer conductor carry equal currents in opposite directions. The magnetic field is zero.
outside the cable
inside the inner conductor
inside the outer conductor
in between the two conductor
The correct Answer is:A
To solve the problem of finding the magnetic field in a coaxial straight cable with equal currents in opposite directions, we can follow these steps:
Step 1: Understand the Configuration
We have a coaxial cable consisting of a central conductor and an outer conductor. The central conductor carries a current I in one direction, while the outer conductor carries an equal current I in the opposite direction.
Step 2: Draw the Diagram
Draw a diagram to represent the coaxial cable. Label the central conductor and the outer conductor. Indicate the direction of the currents in both conductors. The central conductor can be represented with a dot (indicating current coming out of the page), and the outer conductor can be represented with an 'X' (indicating current going into the page).
Step 3: Apply Ampere's Circuital Law
We will use Ampere's Circuital Law, which states:
∮B⋅dl=μ0Iin
where Iin is the current enclosed by the Amperian loop.
Step 4: Consider Different Regions
1. Inside the Inner Conductor: The magnetic field inside a solid conductor is determined by the current flowing through it. However, since we are looking for the magnetic field outside the outer conductor, we can skip this region.
2. Between the Conductors: In this region, the magnetic field due to the inner conductor is directed in one way, while the magnetic field due to the outer conductor is directed in the opposite way. Since the currents are equal and opposite, the magnetic fields will cancel each other out.
3. Outside the Outer Conductor: For a point outside the cable, we can apply Ampere's Law again. The total current enclosed by the Amperian loop in this region is zero because the equal and opposite currents cancel each other out.
Step 5: Calculate the Magnetic Field
For a point outside the coaxial cable, the enclosed current Iin=I−I=0. Thus, applying Ampere's Law:
∮B⋅dl=μ0⋅0=0
This implies that the magnetic field B at any point outside the coaxial cable is zero.
Conclusion
The magnetic field in the coaxial cable configuration, where the central and outer conductors carry equal currents in opposite directions, is zero outside the cable.
---
We have a coaxial cable consisting of a central conductor and an outer conductor. The central conductor carries a current I in one direction, while the outer conductor carries an equal current I in the opposite direction.
Draw a diagram to represent the coaxial cable. Label the central conductor and the outer conductor. Indicate the direction of the currents in both conductors. The central conductor can be represented with a dot (indicating current coming out of the page), and the outer conductor can be represented with an 'X' (indicating current going into the page).
We will use Ampere's Circuital Law, which states:
∮B⋅dl=μ0Iin
where Iin is the current enclosed by the Amperian loop.
1. Inside the Inner Conductor: The magnetic field inside a solid conductor is determined by the current flowing through it. However, since we are looking for the magnetic field outside the outer conductor, we can skip this region.
2. Between the Conductors: In this region, the magnetic field due to the inner conductor is directed in one way, while the magnetic field due to the outer conductor is directed in the opposite way. Since the currents are equal and opposite, the magnetic fields will cancel each other out.
For a point outside the coaxial cable, the enclosed current Iin=I−I=0. Thus, applying Ampere's Law:
∮B⋅dl=μ0⋅0=0
This implies that the magnetic field B at any point outside the coaxial cable is zero.
The magnetic field in the coaxial cable configuration, where the central and outer conductors carry equal currents in opposite directions, is zero outside the cable.
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - exercise
60 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 1
12 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
Similar Questions
A coaxial cable consists of a thin inner conductor fixed along the axis of a hollow outer conductor. The two conductor carry equal currents in opposite directions. Let B1andB2 be the magnetic fields in the region between the conductors and outside the conductor, respectively. Then,
View SolutionConsider a coaxial cable which consists of an inner wire of radius a surrounded by an outer shell of inner and outer radii b and c respectively. The inner wire carries an electric current i0 and the outer shell carries an equal current in opposite direction. Find the magnetic field at a distance x from the axis where (a) x<a, (b) a<x<b, (c) b<x<c and (d)x>c. Assume that the current density is uniform in the inner wire and also uniform in the outer shell.

View Solution
Knowledge Check
The two linear parallel conductors carrying currents in the opposite direction…………………each other.
AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is the correct explanation of assertion.CIf assertion is true but reason is falseDIf both assertion and reason are false.
An otherwise infinite, straight wire has two concentric loops of radii a and b carrying equal currents in opposite directions as shown in Fig. The magnetic field at the common centre is zero for
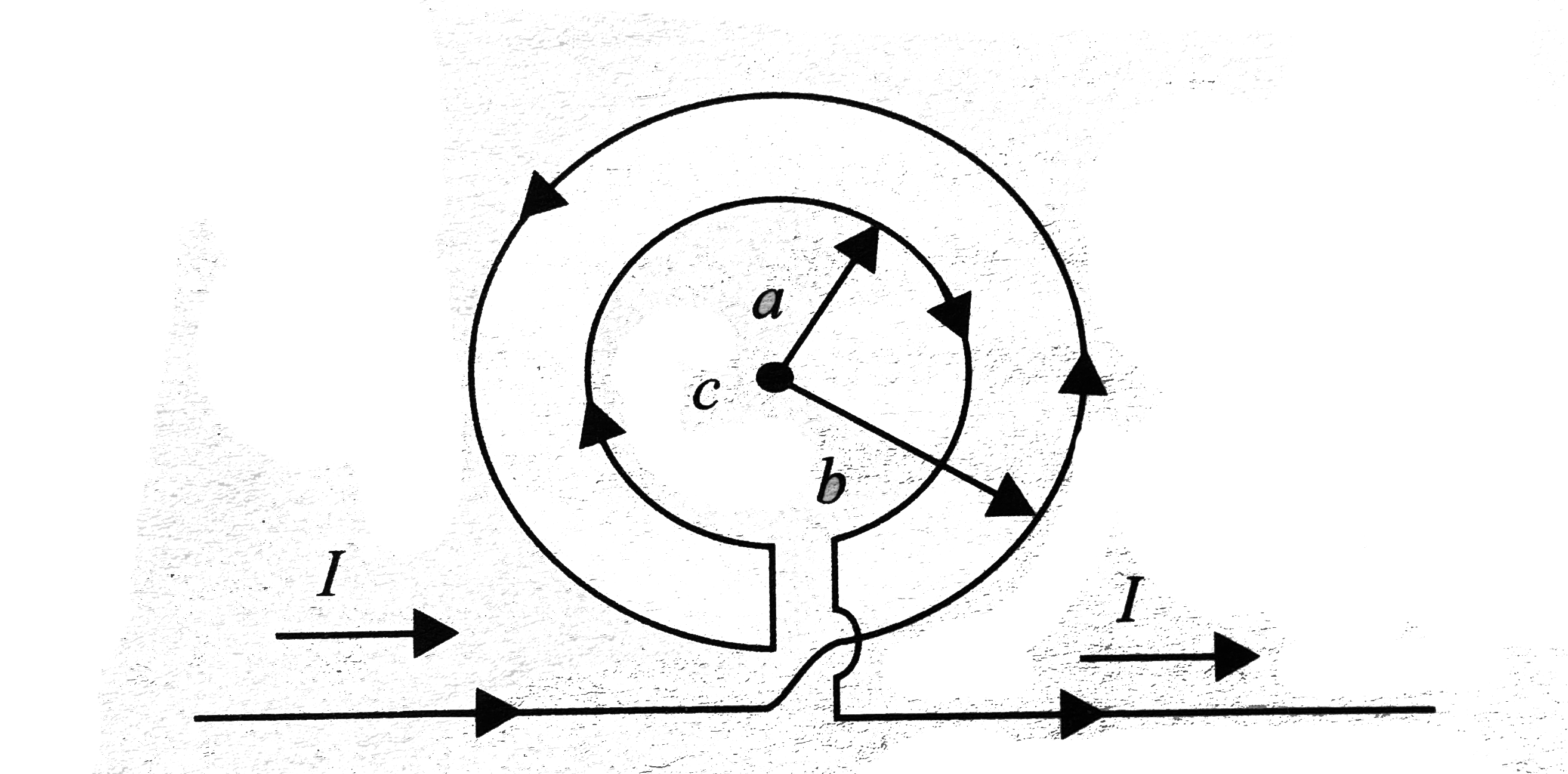
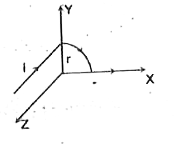
View SolutionShown in the figure is a conductor carrying a current i. the magnetic field at the origin is :
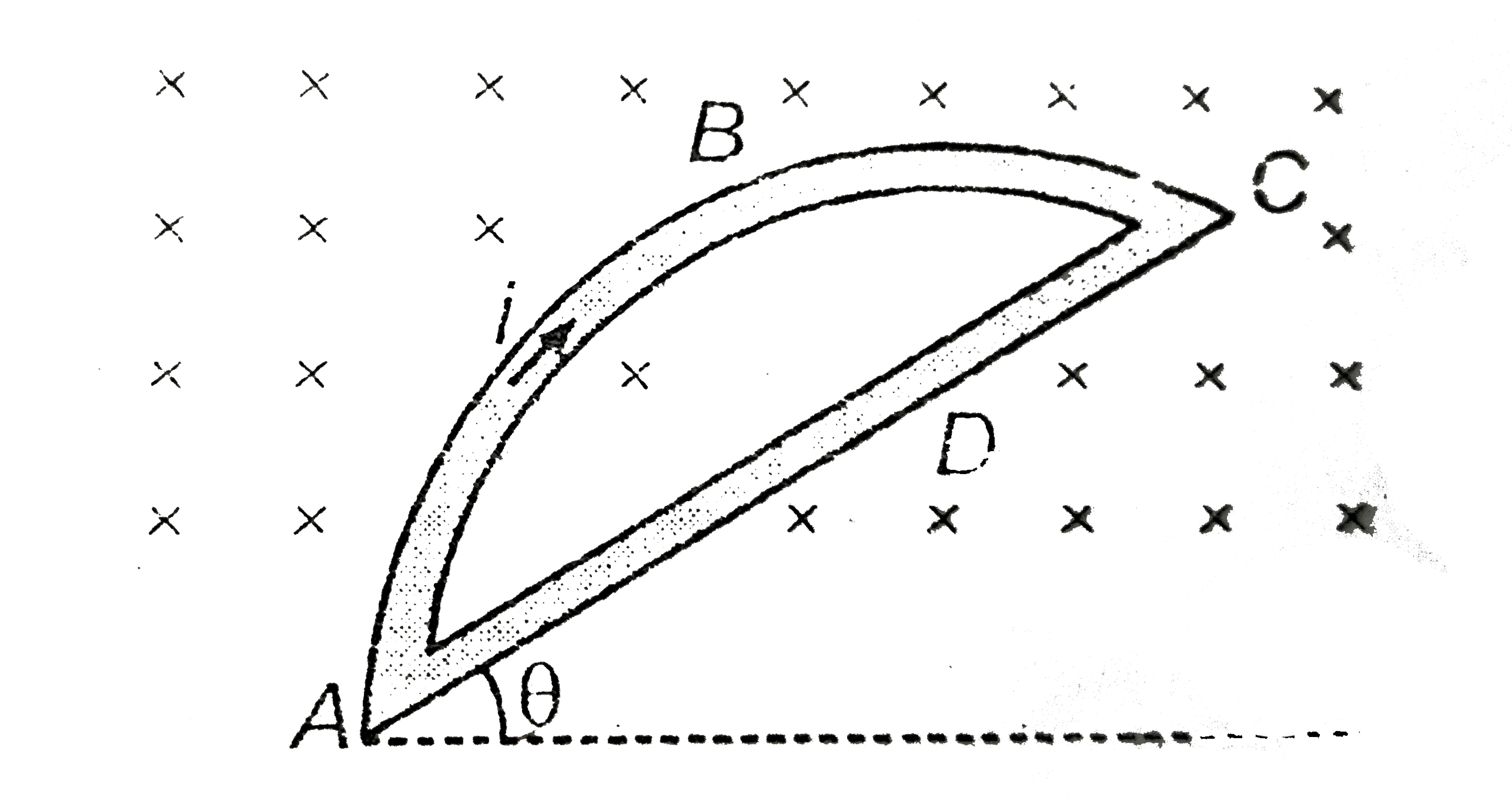
View SolutionA circular wire ABC and a straight conductor ADC are carrying current i and are kept in the magnetic field B then
View SolutionA coaxial cable made up of two conductors. The inner conductor is solid and is of radius R1 and the outer conductor is hollow of inner radius R2 and outer radius R3. The space between the conductors is filled with air. The inner and outer conductors are carrying currents of equal magnitudes and in opposite directions. Then the variation of magnetic field with distance from the axis is best plotted as
View SolutionA coaxial cable made up of two conductors. The inner conductor is solid and is of radius R1 and the outer conductor is hollow of inner radius R2 and outer radius R3. The space between the conductors is filled with air. The inner and outer conductors are carrying currents of equal magnitudes and in opposite directions. Then the variation of magnetic field with distance from the axis is best plotted as
View SolutionA coaxial cable made up of two conductors. The inner conductor is solid and is of radius R1 and the outer conductor is hollow of inner radius R2 and outer radius R3. The space between the conductors is filled with air. The inner and outer conductors are carrying currents of equal magnitudes and in opposite directions. Then the variation of magnetic field with distance from the axis is best plotted as
View SolutionThe figure shows the cross section of two long coaxial tubes carrying equal current I in opposites directions. If B1 and B2 are magnetic fields at point 1 and 2 as shown in figure then

View Solution
