A tightly- wound solenoid of radius a and length l has n turns per unit length. It carries an electric current i. Consider a length dx of the solenoid at a distance x from one end. This contains n dx turns and may be approximated as a circular current I n dx. (a) Write the magnetic field at the centre of the solenoid due to this circular current. Integrate this expression under proper limits to find the magnetic field at the centre of the solenoid. (b) Verify that if l>>a, the field tends to (B=(μ0)ni) and if a>>1, the field tends toB=((μ0)nil2a) . Interpret these results. Solution in Gujrati
(a) Magnetic field at centre due to circular <br> loop<br>B = int dB<br>=int_(0)^1 ((mu_0a^2nidx)/(4pi[(a^2+(l-2x)^2 )]^(3//2))<br>=int_(0)^1 ((mu_0 nia^2 dx)/(4pia^3[1+((l-2x)/(a))^2] ^(3//2))<br>=((mu_0ni) /(4pi a)(int_(0)^1) (dx)/([1+((l-2x)/(a)^2)]^(3/2)<br> = ((mu_0 ni)/(4pia). ((4pi a )/(sqrt 1+(2a)/(l))) = (mu_0ni) /(sqrt (1+((2a)/(l)^2)))) <br>(b)When agtgtl <br>Then B = mu_(0)ni /2a.
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises
61 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Exercises
9 Videos
Similar Questions
The magnetic field at the origin due to a current element I (→dl) placed at a positon (→r) is
View SolutionAn alpha particle is projected vertically upward a speed of 3.0X104kms−1 in a region where a magnetic field of magnitude 1.0 T exists in the direction south to north. Find the magnetic force that acts on the a particle.
View SolutionThe magnetic intensity H at the centre of a long solenoid carrying a current of 2.0A, is found to be 1500Am−1. Find the number of turns per centimetre of the solenoid.
View SolutionA tightly- wound solenoid of radius a and length l has n turns per unit length. It carries an electric current i. Consider a length dx of the solenoid at a distance x from one end. This contains n dx turns and may be approximated as a circular current I n dx. (a) Write the magnetic field at the centre of the solenoid due to this circular current. Integrate this expression under proper limits to find the magnetic field at the centre of the solenoid. (b) Verify that if l>>a, the field tends to (B=(μ0)ni) and if a>>1, the field tends toB=((μ0)nil2a) . Interpret these results.
View SolutionThe magnetic field B with in the solenoid having n turns per metre length and carrying a current of i ampere is given by
View SolutionA long solenoid has a radius a and number of turns per unit length is n . If it carries a current i, then the magnetic field on its axis is directly proportional to
View SolutionDerive an expression for the axial field of a solenoid of radius ''a'', containing ''n'' turns per unit length and carrying current ''I''.
View SolutionA solenoid of radius R number of turn per unit length n and length L has a current I=I0cosωt. The value of induced electric field at a distance of r outside the solenoid, is :
View SolutionThe magnetic field B within a solenoid of length L with N turns and carrying a current I is given by
View SolutionA tightly wound solenoid of radius 'a' and length 'l' has n turns per unit length. It carries an electric current i. Magnetic field at a distance l4 from one of the end (inside the solenoid on its axis) is B=μ0ni(√5+3)√K for l=4a. Then find the value of K.
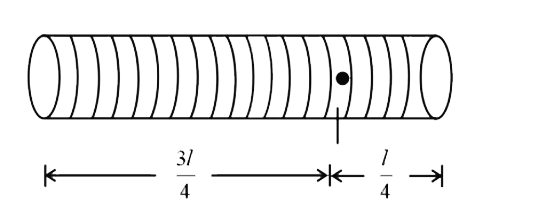
View SolutionThe magnetic field B within the solenoid having n turns per unit length and carrying a current I is given by
View SolutionA very long solenoid of length L has n layers. There are N turns in each layer. Diameter of the solenoid is D and it carries current I. The magnetic field at the centre of the solenoid is ______
View SolutionA tightly- wound solenoid of radius a and length l has n turns per unit length. It carries an electric current i. Consider a length dx of the solenoid at a distance x from one end. This contains n dx turns and may be approximated as a circular current I n dx. (a) Write the magnetic field at the center of the solenoid due to this circular current. Integrate this expression under proper limits to find the magnetic field at the center of the solenoid. (b) Verify that if l>>a, the field tends to (B=(μ0ni) and if a>>1, the field tends toB=((μ0)nil2a) . Interpret these results.
View SolutionGive the expression for magnetic field well inside a long solenoid having n turns per length carrying a current I.
View SolutionA long solenoid has a radius a and number of turns per unit length is n. If it carries a current i, then the magnetic field on its axis is directly proportional to
View SolutionA tightly wound solenoid of radius 'a' and length 'l' has n turns per unit length. It carries an electric current i. Magnetic field at a distance l4 from one of the end (inside the solenoid on its axis) is B=μ0ni(√5+3)√K for l=4a. Then find the value of K.

View Solution
