Calculate the dimensions of (a) ∫→E.d→l,(b)vBlanddΦ0dt. The symbols have their usual meanings.Solution in Gujrati
(a)∫E/dl=MLT−3I−1×L=ML2I−1T−3
(b)vBl=LT−1×MI−1T−2×L
=ML2I−1T−3
(c)dϕdt=MI−1T−2×L×LT−1
=ML2I−1×ML2×T−3.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE9videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 210videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises75videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises9videos
ELECTROMAGNETIC WAVES
Similar Questions
Shown a metallic square frame of edga a in a vertical plane. A uniform magnetic field B exists in the space in a directon perpendicular to the plane of the figure. Two boys pull the opposite corners of the square ot deform it into a rhombus. They start pulling the corners t t=0 and sisplace the corners at a uniform speed u. (a) find the induced emf in the frame at the instant when the angles at these corners reduce to 60∘. (b) find the induced current in the frame at this instatnt if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
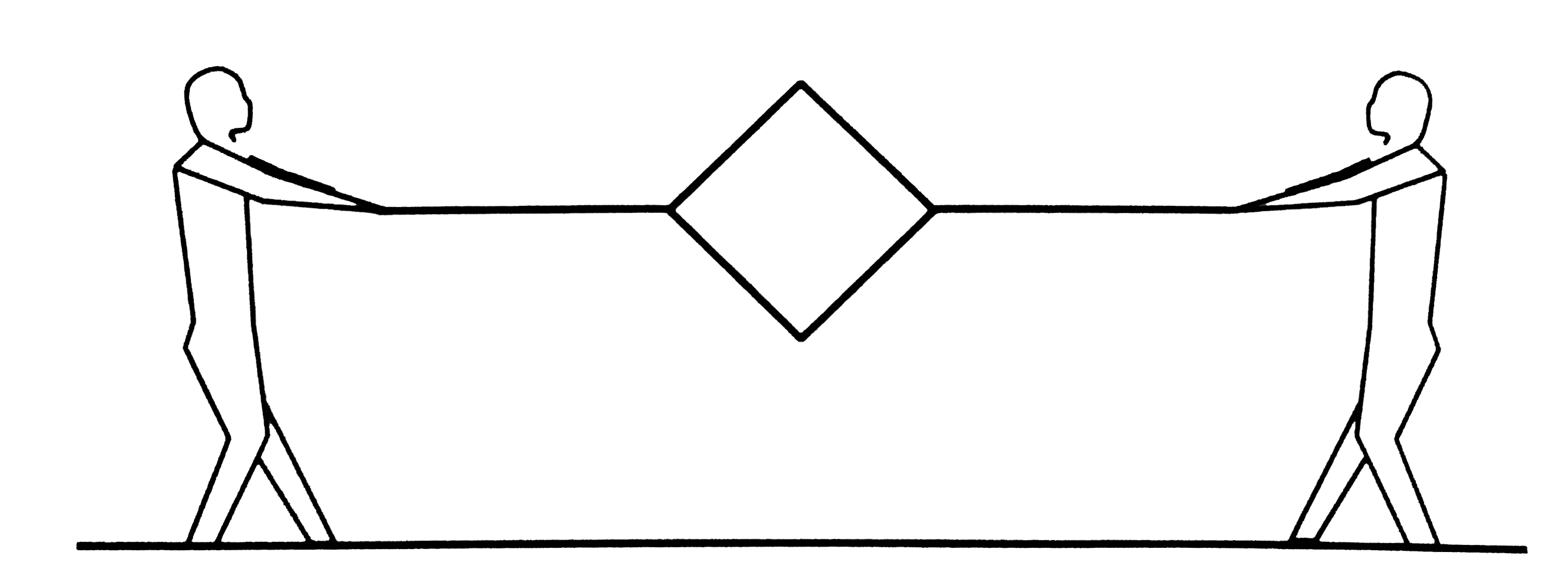 02:01View Solution
02:01View SolutionA bar magnet is moved along the axis of a copper ring placed far away from the magnet. Looking from the side of the magnet, an anticlockwise current is found to be induced in the ring. Which of the following may be true?
01:27View SolutionFind the dimensional formula of ε0 .
03:35View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
01:24View SolutionCalculate the dimensions of (a) ∫→E.d→l,(b)vBlanddΦ0dt. The symbols have their usual meanings.
02:06View SolutionFind the dimension of the quantity L/(RCV), where symbols have usual meaning.
03:14View SolutionThe dimension of e2/ε0hc (here symbols have their usual meanings) are
02:27View SolutionGiven →F=→at where symbols have their usual meaning. The dimensions of a is .
View SolutionDimensions of 1μ0∈0 , where symbols have their usual meaning are
View SolutionCalculate the dimensions of (a) ∫→E.d→l,(b)vBlanddΦ0dt. The symbols have their usual meanings.
02:06View SolutionIn the following 'I' refers to current and other sumbols have their usual meaning . Choose the option that corresponding to the dimensions of electrical conductivity :
04:14View SolutionDimension of (1)/mu_0epsilon_0 where symbols have their usual meanings are:
03:13View SolutionDimensions of (1)/mu_0epsilon_0 where symbols have their usual meanings are:
01:15View SolutionDimensions of 1μ0∈0 , where symbols have their usual meaning are
01:01View SolutionThe dimension of e2/ε0hc (here symbols have their usual meanings) are
01:53View SolutionIn the following 'I' refers to current and other symbols have their usual meaning. Chosse the option that corresponds to the dimensions of electrical conductivity:
01:18View Solution

