(a) the magnetic field in a region varies as shown in . Calculate the average induced emf in a conducting loop of area 2.0X10^(-3) m^2 placed perpendicular to the field in each of the10ms intervals shown. (b) In which intervals is the emf not constant? Neglect the behaviour near the ends of 10 ms intervals.
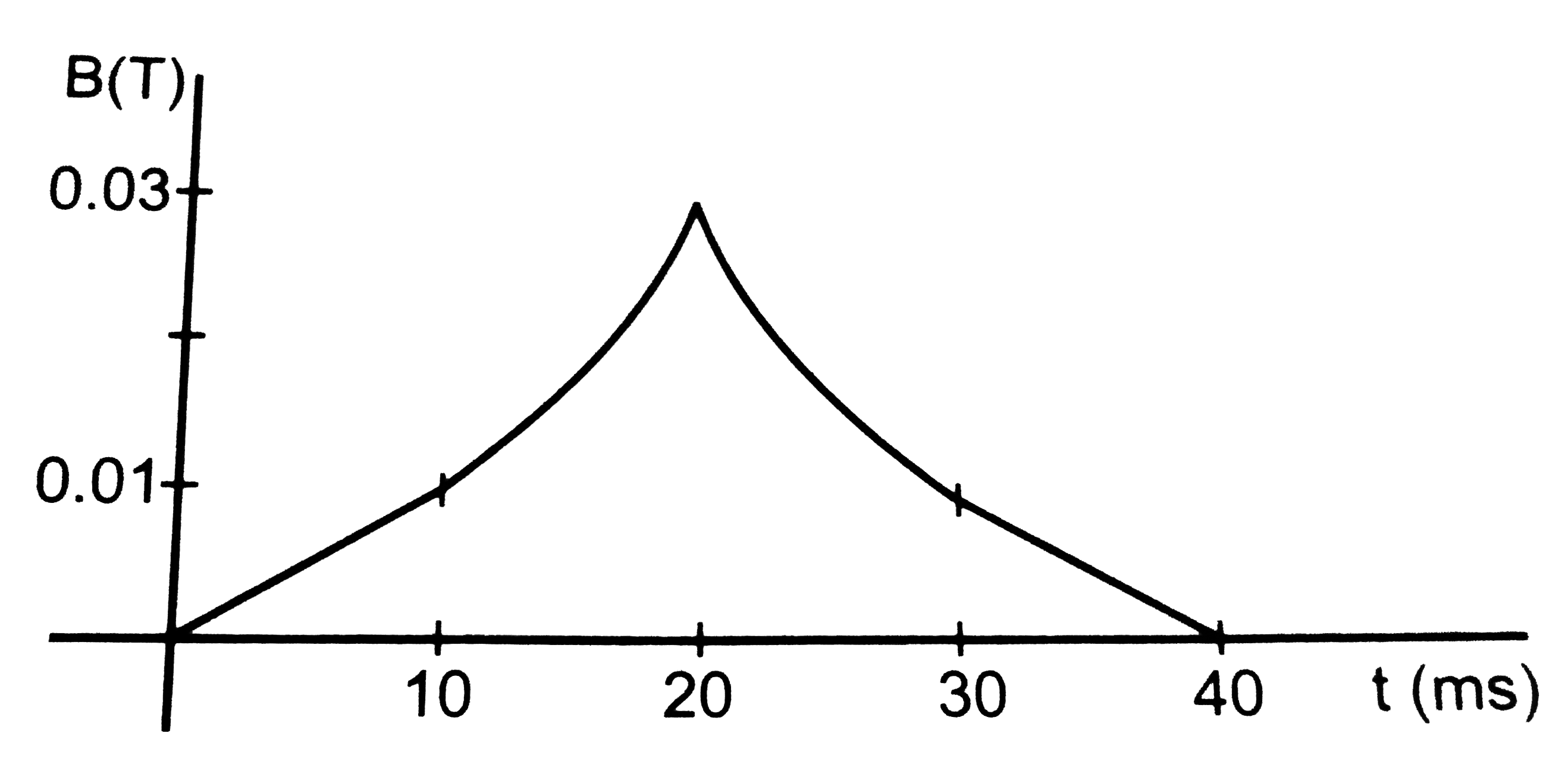
(a)ϕ2=B.A=00.01×2×10−3
=2×10−5[sinceϕ1=0]
dϕ=2×10−5
e=−dϕdt=−2×10−510×10−3
=2×10−3=−2mV
ϕ3=B.A=0.04×2×10−3
=6×10−5
dϕ=4×10−5
e=−dϕdt=−4mV
ϕ4=B.A=0.01×2×10−3
=2×10−5
dϕ=−4×10−5
e=−dϕdt=4mV
ϕ5=B.A=0
dϕ=−2×10−5
e=−dϕdt=−(−2)×10−510×10−3=2mV.
(b)Emfis¬constantiscaseof→10−20msand20ms−30msas−4mVand4m.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises
9 Videos
Similar Questions
(a) the magnetic field in a region varies as shown in . Calculate the average induced emf in a conducting loop of area 2.0X10^(-3) m^2 placed perpendicular to the field in each of the10ms intervals shown. (b) In which intervals is the emf not constant? Neglect behaviour near the ends of 10 ms intervals.

View Solution(a) The magnetic field in a region varies as shown in figure. Caculate the average induced emf in a conduction loop of area 10−3m2 placed perpendicular to the field in each of the 10ms intervals shown. (b) In which interval(s) I sthe emf not constant ? Neglect the behaviour near the ends of 10 ms intervals.

View Solution
Knowledge Check
A conducting square loop is placed in a magnetic field B with its plane perpendicular to the field. Now the sides of the loop start shrinking at a constant rate α. the induced emf in the loop at an instant when its side is a is
A2aαBBa2αBC2a2αBDaαBa conducting loop of radius R is precent in a uniform magnetic-field B perpendicular the plane of the ring. If radius R varies as a function of time 't', as R0+t. The e.m.f induced in the loop is
 A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzero
A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzeroA single conducting loop with an area of 2.0 m2 rotates in a uniform magnetic field so that the induced emf has a sinusoidal time dependence as shown.
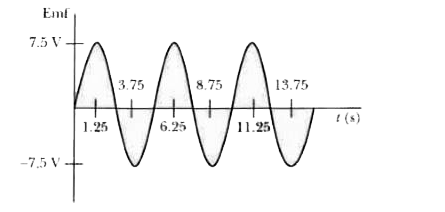
What is the period of the induced current?A1.25 sB3.75 sC2.50 sD5.00 s
A rectangular coil of area 50cm2 and 100 turns is placed perpendicular to a magnetic field of 10−2Wb/m2. If the coil is withdrawn from the field in 40 ms, calculate the emf induced.
View SolutionA coil having an area 2m2 is placed in a magnetic field which changes from 1wb/m2 n interval of 2s. The e.m.f. induced in the coil is:
View SolutionA conducting square loop is placed in a magnetic field B with its plane perpendicular to the field. Now the sides of the loop start shrinking at a constant rate α. the induced emf in the loop at an instant when its side is a is
View SolutionA semicircular conducting wire of radius a is moving perpendicular to a uniform magnetic field B with speed√2vas shown in the figure.The emf induced across the wire Is
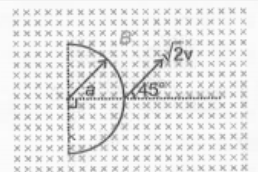
View SolutionA conducting wire of length 10 cm is moving perpendicular in a region of magnetic field 1 tesla with a speed of 10ms−1. Calculate the induced emf in the conductor.
View Solution
