The electric field associated with a light wave is given by E=E0sin[(1.57x107m−1(x−ct)]. Find the stopping potential when this light is used in an experiment on photoelectric affect with a metal having work - function 1.9 eV.Solution in Gujrati
Given, E = E_0 sin [(1.57 xx 10(7) m ^(-1) ) ( x - ct )]<br> w = 1.57 xx 10^(7) xx c <br> rArr f = 1.57 xx 10^(7) xx 3 xx 10^(8) / 2 pi Hz <br> W_0 = 1.9eV <br>NoweV0=hv−W0
=4.14×10−15×(1.57×3×10152π)−1.9eV
=3.105−1.9=1.205V
V_0 = 1.205 xx 1.6 xx 10^(-19) / 1.6 xx 10^(-19) <br> 1.205 V
Topper's Solved these Questions
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMACHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - Exercise
2 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMACHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - Objective 2
7 Videos
- PERMANENT MAGNETSBOOK - HC VERMACHAPTER - PERMANENT MAGNETSEXERCISE - Exercises
25 Videos
- PHOTOMETRYBOOK - HC VERMACHAPTER - PHOTOMETRYEXERCISE - Exercises
16 Videos
Similar Questions
The work function of a metal is 2,5×(10−19)J. (a) Find the threshold frequency for photoelectric emission. (b) If the metal is exposed to a light beam of frequency (6.0×1014) Hz, what will be the stopping potential ?
View SolutionWhen the intensity of a light source is increased
(a) the number of photons emitted by the source in unit time increases
(b) the total energy of the photons emitted per unit time increases
(c) more energetic photons are emitted
(d) faster photons are emitted
View SolutionA long bar magnet has a pole strength of 10Am. Find the magnetic field at a point on the axis of the magnet at a distance of 5cm from the north pole of the magnet.
View SolutionA source emits 45 joules of energy in 15 s. What is the radiant flux of the source ?
View SolutionLight in incident on a metal plate whose work function is 2 eV. Electric field associated with light is given by E=E_(0)sin(omegat-(2pi)/(5xx10^(7))x) { S.I unit} if energy of photom is given by (12375)/(lamda("in"A)) eV then stopping potential is
View SolutionFigure is the plot of the stopping potential versus the frequency of the light used in an experiment on photoelectric effect. Find (a) the ratio h/e and (b) the work function.
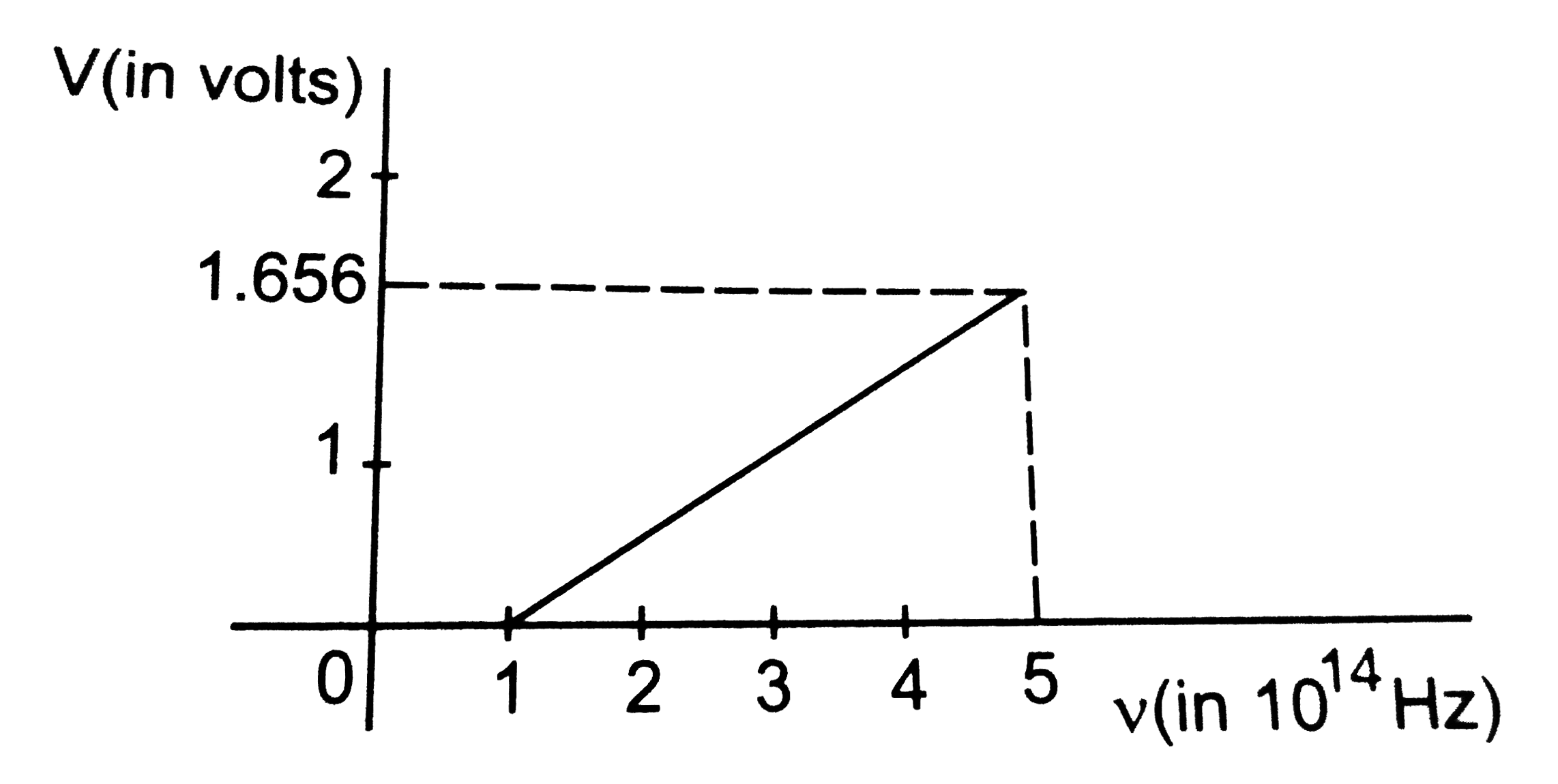
View SolutionThe electric field associated with a light wave is given by E=E0sin[(1.57x107m−1(x−ct)]. Find the stopping potential when this light is used in an experiment on photoelectric affect with a metal having work - function 1.9 eV.
View SolutionIn an experiment on photoelectric effect the frequency f of the incident light is plotted against the stopping potential V_(0) . The work function of the metal is given by ( e is the electronic charge)
View SolutionThe electric field associated with a light wave is given by E=E0sin[(1.57×107m−1)(ct−x)]. Find the stopping potential when this light is used in an experiment on a photoelectric effect with the emitter having work function 2.1eV. h=6.62×10−34Js.
View SolutionThe photoelectric work function for potassium is 2 eV . The light of wavelength 3.6 xx 10^(-7) m falls on potassium . The stopping potential is
View SolutionThe electric field associated with a light wave is given by E=E_0sin [(1.57xx10^7)(x-ct)] (where x and t are in metre and second respectively ). This light is used in an experiment having work function phi=1.9eV. what is the ejected photoelectron ? [ Take pi=3.14, hc = 12400 eVÅ]
View SolutionThe electric field associated with a light wave is given by E=E0sin[(1.57×107m−1(x−ct)]. Find the stopping potential when this light is used in an experiment on photoelectric effect with a metal having work - function 1.9 eV.
View SolutionFigure is the plot of the stopping potential versus the frequency of the light used in an experiment on photoelectric effect. Find (a) the ratio h/e and (b) the work function.

View SolutionLight in incident on a metal plate whose work function is 2 eV. Electric field associated with light is given by E=E0sin(ωt−2π5×107x){ S.I unit} if energy of photom is given by 12375λ(inA) eV then stopping potential is
View SolutionThe electric field of light wave is given as vec(E )=10^(-3)cos((2pi x)/(5xx10^(-7))-2pixx6xx10^(14)t)hat(x)(N)/(C ) This light falls on a metal plate of work function 2eV. The stopping potential of the photo-electrons is : Given E (in eV) = (12375)/(lambda("in"Å))
View SolutionThe electric field associated with a light wave is given by E=E0sin[(1.57x107m−1(x−ct)]. Find the stopping potential when this light is used in an experiment on photoelectric affect with a metal having work - function 1.9 eV.
View Solution
