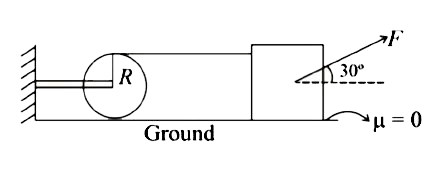
As shown in the figure a block of mass 1 kg connected with a pulley of mass 1 kg and radius 10 cm is acted upon by a variable force of F = kt, as shown. Angular acceleration of pulley when block leaves the contact with ground is:
50√3rad/s2
20√3rad/s2
200√3rad/s2
5√3rad/s2
The correct Answer is:C
Resolving F
Fcos30∘−T=ma….. (i)
Fsin30∘+N=mg……. (ii)
For the time it leaves the contact
Fsin30∘=mg
F = 2mg
T.R. =Iα
2mgcos30−T=mrα
T=√3mg−mrα
T.R.=I.α.
{√3×1×10−1×0.1α}×0.1=1×0.012×α
α=200√3rad/s2
Topper's Solved these Questions
Similar Questions
Knowledge Check
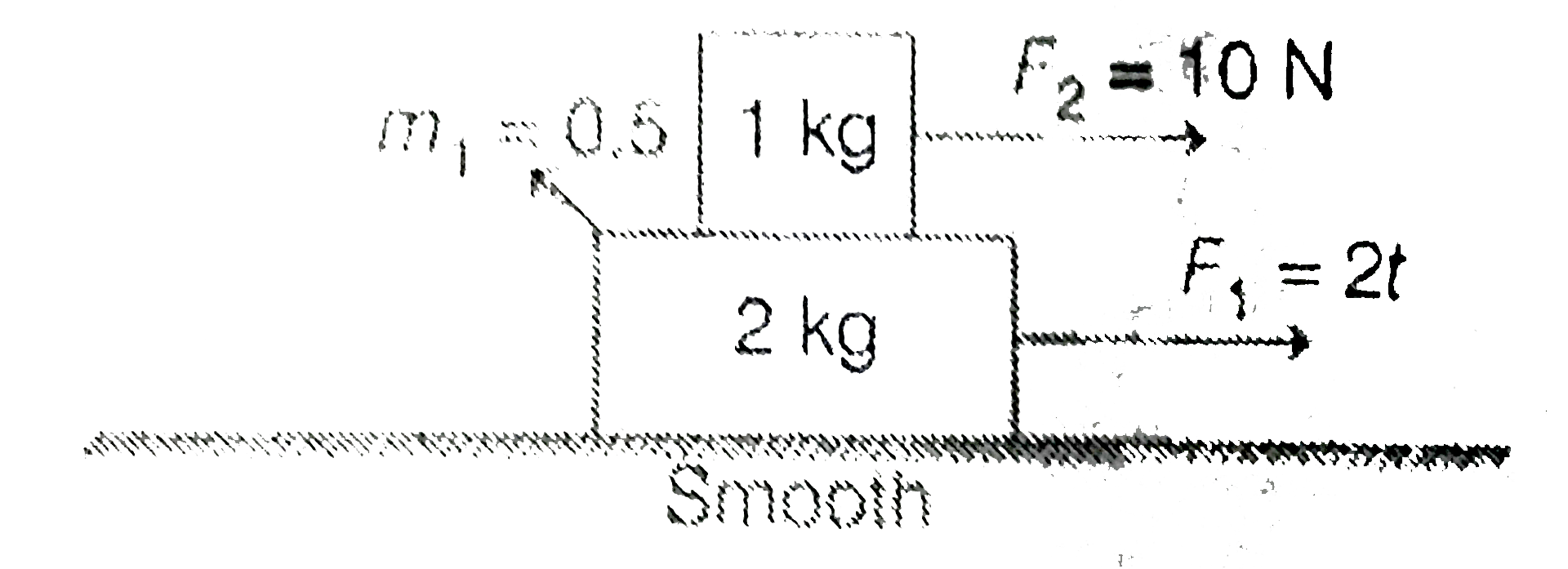
In the figure shown, block of mass 2 kg is very long. Force of friction on 1 kg block is
 Aalways towards rightBalways towards leftCis first towards right and then towards leftDis first towards left and then towards right
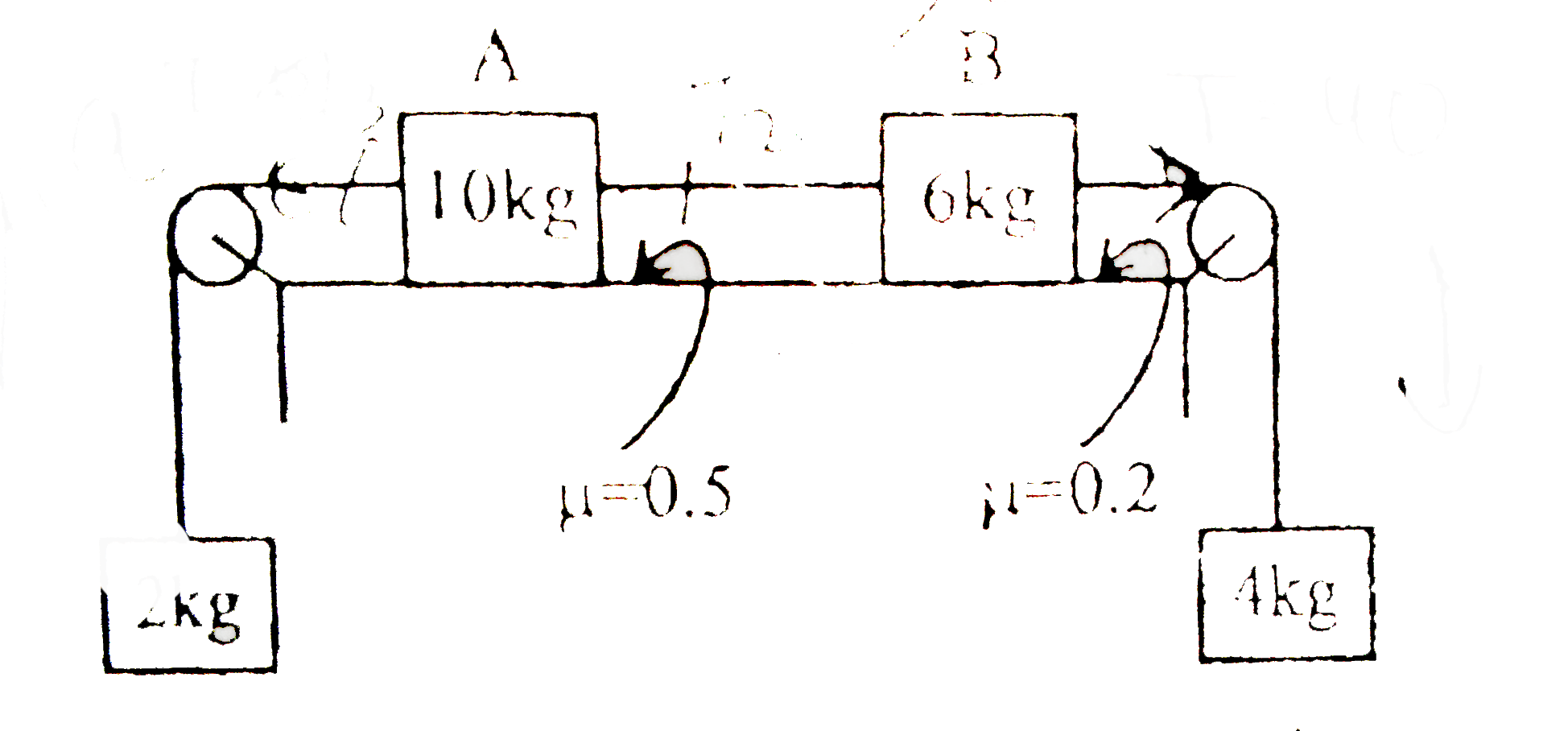
Aalways towards rightBalways towards leftCis first towards right and then towards leftDis first towards left and then towards rightTwo Block A and B of masses 10kg and 6kg respectively are connected through pulley as shown in figure. Find acceleration of block A.
 A0B76C1011D3011
A0B76C1011D3011In the figure shown, all surfaces are smooth and the pulley is massless. A constant force of magnitude F=mg2 is acting on the block of mass M. The acceleration of the block M is :
 Amg2(m+M) towards rightBmg2(m−M) towards rightsCmg2(m−M) towards leftDmg2(m+m) toward left
Amg2(m+M) towards rightBmg2(m−M) towards rightsCmg2(m−M) towards leftDmg2(m+m) toward left
In the figure shown, block of mass 2 kg is very long. Force of friction on 1 kg block is

View SolutionA block of mass 5kg is resting on a rough surface as shown in the figure. It is acted upon by a force of F towards right. Find frictional force acting on block when 25N.
View SolutionIn the figure shown, all surfaces are smooth and the pulley is massless. A constant force of magnitude F=mg2 is acting on the block of mass M. The acceleration of the block M is :

View SolutionA string is wrapped on a wheel of moment of inertia 0.20 kg-m^2 and radius 10 cm and goes through a light pulley to support a block of mas 2.0 kg as shown in figure. Find the acceleration of the block.
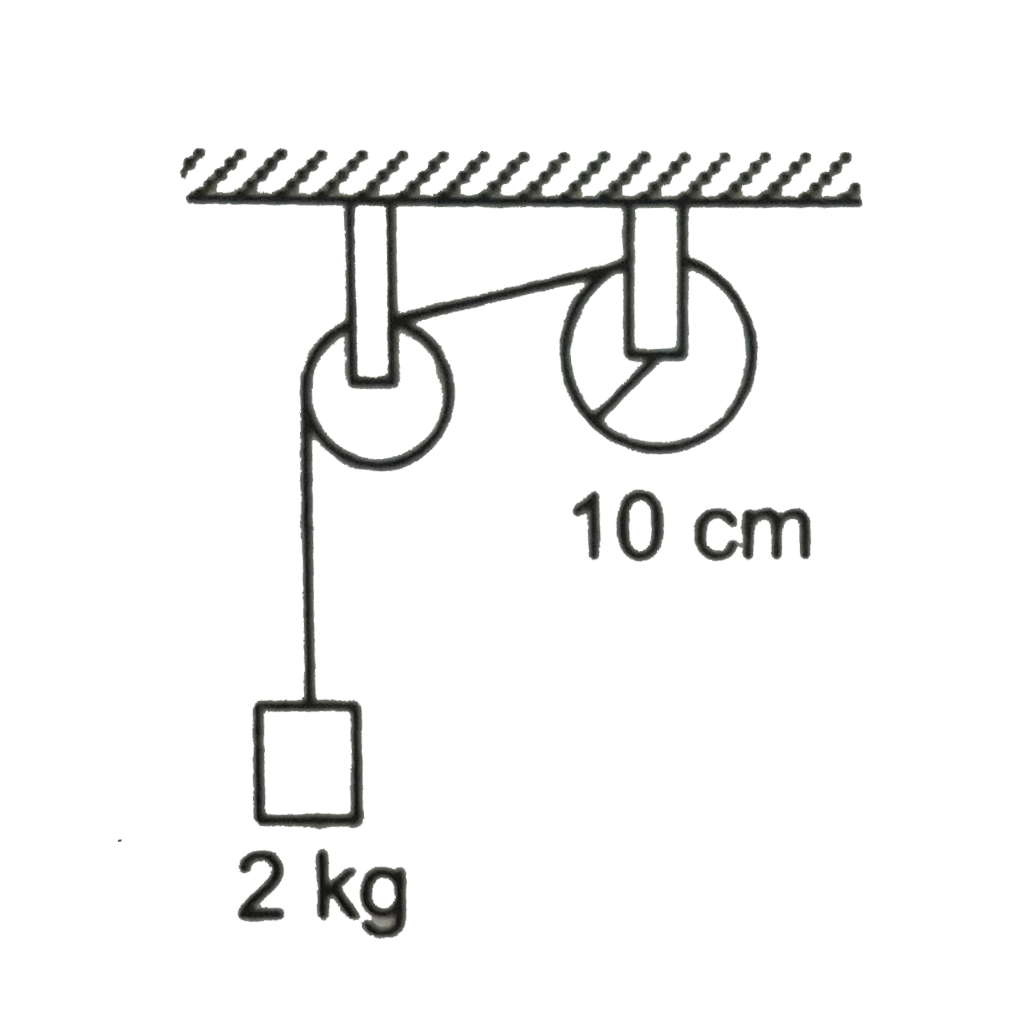
View SolutionA string is wrapped on a wheel of moment of inertia 0.20 kg-m^2 and radius 10 cm and goes through a light pulley to support a block of mass 2.0 kg as shown in figure. Find the acceleration of the block.

View Solution