CD and GH are respectively the bisectors of and of and respectively. If show that :
Step by step video & image solution for CD and GH are respectively the bisectors of angleACB and angleEGF of DeltaABC and DeltaEFG respectively. If DeltaABC ~ DeltaFEG show that : DeltaDCA~ DeltaHGF by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - NCERT CORNER ( TEXTBOOK QUESTIONS) ( EXERCISE - 6.4 )
9 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - NCERT CORNER ( TEXTBOOK QUESTIONS) ( EXERCISE - 6.5 )
23 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - NCERT CORNER ( TEXTBOOK QUESTIONS) ( EXERCISE - 6.2 )
12 Videos
- SURFACE AREAS AND VOLUMES BOOK - OSWAL PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - BOARD CORNER (LONG ANSWER TYPE QUESTIONS)
9 Videos
Similar Questions
In the given figure, CD and GH are respectively the bisectors of ∠ACBand∠FGEofΔABCandΔEFG respectively . If ΔABC~ΔFEG, prove that :
(a) ΔADC~ΔFHG (b)ΔBCD~ΔEGH (c)CDGH=ACFG
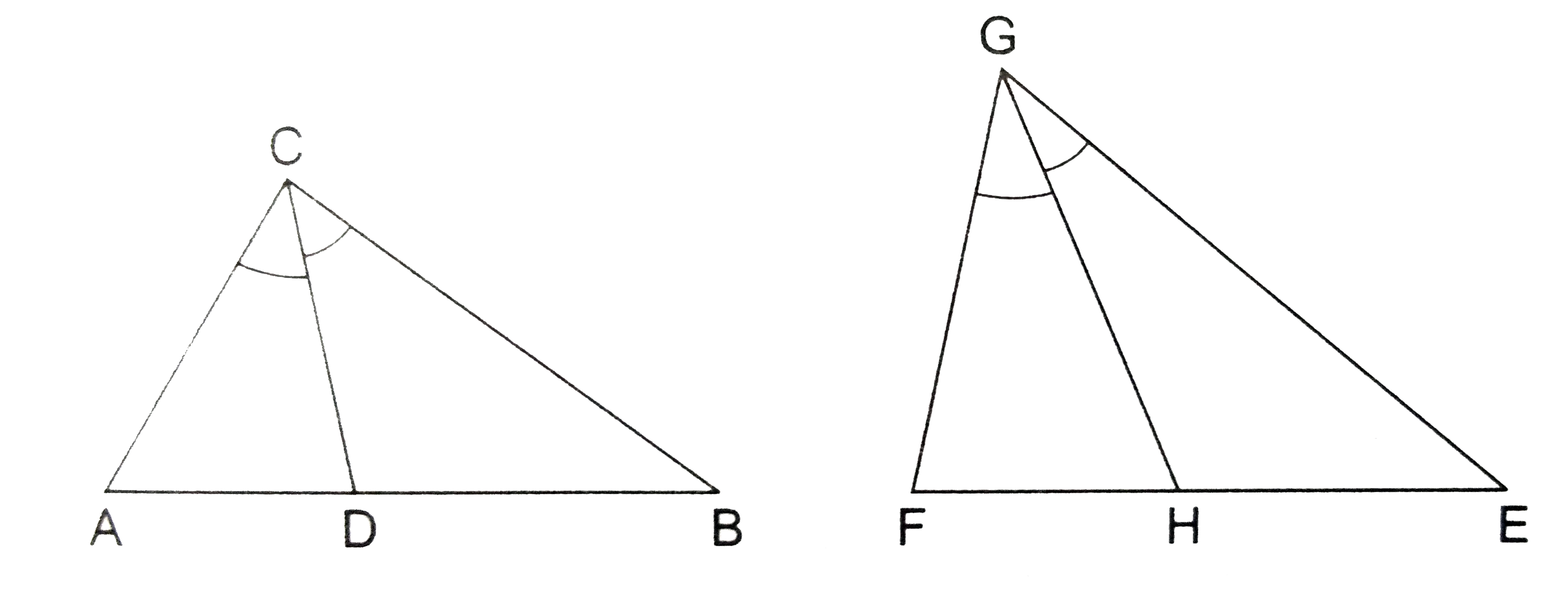
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG show that :
ΔDCB~ΔHGE
View Solution
Knowledge Check
Find the value of x and y respectively, if ΔABC≅ΔQRP.
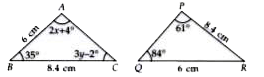 A15∘,30∘B21∘,40∘C30∘,15∘D40∘,21∘
A15∘,30∘B21∘,40∘C30∘,15∘D40∘,21∘D, E and Fare respectively the midpoints of the sides of ΔABC. Which of the following is true?
 AArea of ΔDEF= Area of ΔABCBArea of ΔDEF=12 Area of ΔABCCArea of ΔDEF= 13Area of ΔABCDArea of ΔDEF=14 Area of ΔABC
AArea of ΔDEF= Area of ΔABCBArea of ΔDEF=12 Area of ΔABCCArea of ΔDEF= 13Area of ΔABCDArea of ΔDEF=14 Area of ΔABC
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG show that :
CDGH=ACFG
View SolutionIn ΔABC,AB=AC and the bisectors of ∠B and ∠C meet AC and AB at point D and E respectively. Prove that BD=CE.
View SolutionIf ΔABC~ΔZYX, then name the angles equal to ΔB and ΔZ respectively.
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(BDEF) =12ar(△ABC)
View SolutionThe heights of ΔABC and ΔDBC are 4 cm and 6 cm respectively. Find A(ΔABC)A(ΔDBC).
View SolutionE and F are respectively the midpoints of the sides AB and AC of ΔABC and the area of quadrilaterals BEFC is k times the area of ΔABC . Then the values of k
View Solution
