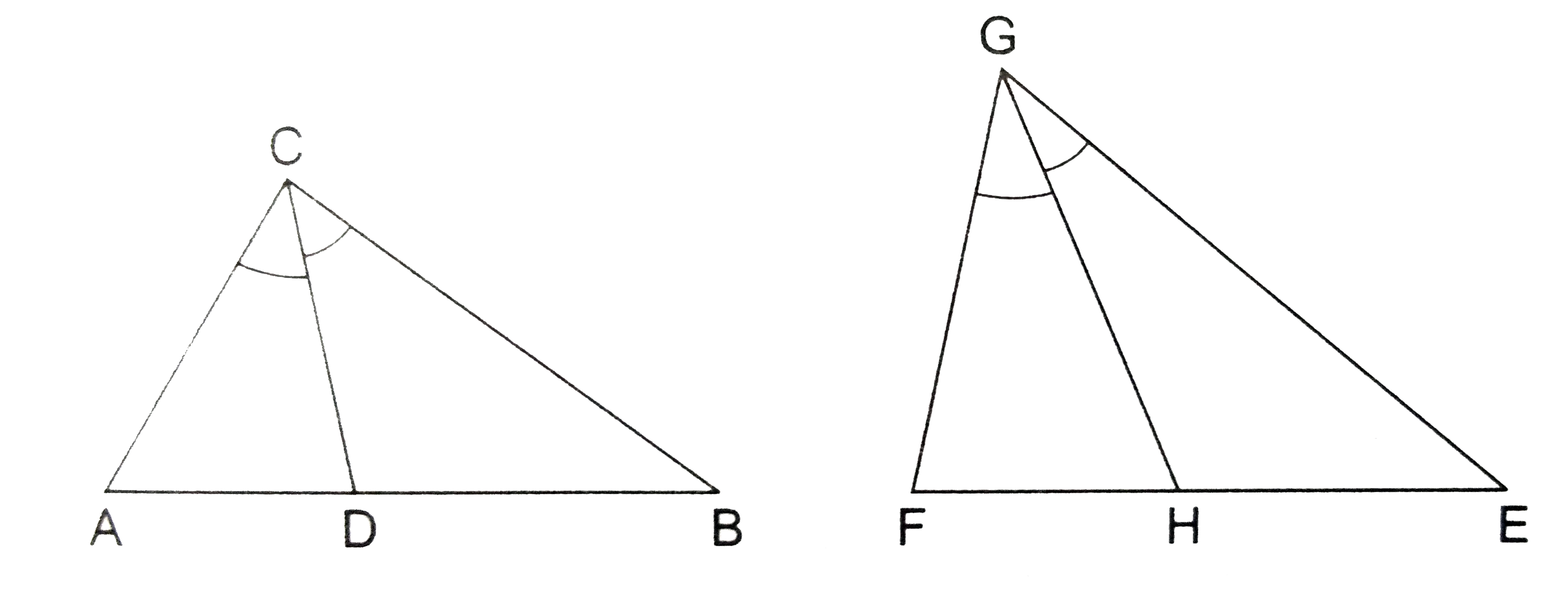
In the given figure, CD and GH are respectively the bisectors of ∠ACBand∠FGEofΔABCandΔEFG respectively . If ΔABC~ΔFEG, prove that :
(a) ΔADC~ΔFHG (b)ΔBCD~ΔEGH (c)CDGH=ACFG
Video Solution
Text Solution
ΔABC~ΔFEG (given)
∴∠ACB=∠FGE [ corresponding angles of similar triangles are equal]
⇒12∠ACD=12∠FGE.
(a) In ΔADCandΔFHG, we have
∠DAC=∠HFG[∴∠A=∠FsinceΔABC~ΔFEG]
and ∠ACD=∠FGH [ proved above]
∴ΔADC~ΔFHG [ by AA- similarity]
(b) In ΔBCDandΔEGH, we have
∠DBC=∠HEG[∴∠B=∠EsinceΔABC~ΔFEG]
and∠DCB=∠HGE [ proved above]
∴ΔBCD~ΔEGH.
(c) We have
ΔADC~ΔFHG [ proved above]
And so, CDGH=ACFG [ crossponding sides of similar triangles are proportional.]
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A1videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7A12videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Test Yourself20videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 1127videos
T-RATIOS OF SOME PARTICULAR ANGLES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself20videos
TRIGONOMETRIC IDENTITIES
Similar Questions
Knowledge Check
- Question 1 - Select One or More
In a triangle, with usual notations, the length of the bisector of angle A is
A2bcb+csinA2B2bcb+ccosA2Cabc2R(b+c)cosecA2D4Ab+ccosecA2 - Question 2 - Select One
In given triangle ABC ,OB and OC are bisectors of ∠Ba nd ∠C respectively then ∠BOC is equal to
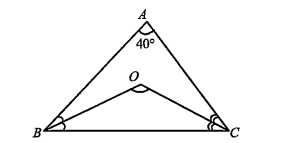 A70∘B110∘C140∘D80∘
A70∘B110∘C140∘D80∘
In the adjoning figure, D and E are the points on the sides AB and AC respectively of ΔABC and area of ΔBCE= area of ΔBCD.
Prove that DE∣∣BC
 View Solution
View SolutionIn the given figure, if ∠D=∠C, then it is true that △ADE~△ACB? Why?
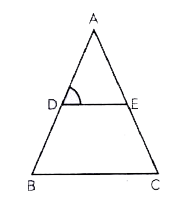 View Solution
View SolutionThe bisectors of the angles B and C of a triangle ABC , meet the opposite sides in D and E respectively. If DE||BC , prove that the triangle is isosceles.
View SolutionIn ΔABC,DandE are the midpoint of AB and AC respectively. Find the ratio of the areas of ΔADEandΔABC.
 View Solution
View SolutionIn the given figure , AB=CD,CE=BF and ∠ACE=∠DBF . Prove that
△ACE≅△DBF
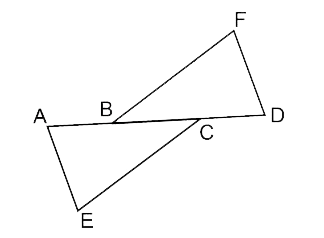 View Solution
View SolutionIn a triangle aBC ,∠B=2∠C.AD and BE bisectors of ∠BACand∠ABC. If AB=CD . Find ∠BAC
View Solution



