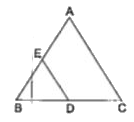
ΔABC तथा ΔBDE दो समबाहु त्रिभुज इस प्रकार हैं कि D, BC का मध्यबिंदु है। तब, ar(ΔBDE):ar(ΔABC)=?
1:2
1:4
√3:2
3:4
The correct Answer is:B
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - BHARATI BHAWANCHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नमाला 11B
2 Videos
- संख्या पद्धति BOOK - BHARATI BHAWANCHAPTER - संख्या पद्धति EXERCISE - प्रश्नमाला 1H (बहुवैकल्पिक प्रश्न)
45 Videos
- सांख्यिकी BOOK - BHARATI BHAWANCHAPTER - सांख्यिकी EXERCISE - प्रश्नमाला 16 E
28 Videos
Similar Questions
एक समांतर चतुर्भुज ABCD की भुजा AB का मध्यबिंदु M है। यदि ar(AMCD)=24cm2है, तो ar(ΔABC) ज्ञात कीजिए।
View Solutionनिम्नलिखित में से कौन सी संख्या परिमेय है ?
View Solutionआँकड़ो 12,,25,15,18,17,20,22,6,16,11,8,19,10,30,20,32 का परिसर है
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=12ar(ΔABC).
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionIn the following figure, AB and BC are equidistant from the centre 'O' of the Show that
(a) ABC is an isosceles triangle.
(b) OB bisects angle ABC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_X_C13_E02_006_Q01.png" width="80%"gt
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionΔABC तथा ΔBDE दो सम्बउ त्रिभुज इस प्रकार है कि भुजा BC का मध्य बिंदु D है | त्रिभुजों ABC और BDE के क्षेत्रफलों का अनुपात है:
View Solutionसत्य/असत्य बताइए तथा उत्तर का औचित्य भी बताइए -
ABC और BDE दो समबाहु त्रिभुज इस प्रकार है की D भुजा BC का मध्य-बिंदु है। तब
ar(BDE)=14ar(ABC).
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=14ar(ΔABC).
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE)=14 ar(ABC).
View Solution
