A very long solenoid of radius R is carrying a current ∣∣(t)=kte−at(k>0),as a function of time (t≥0) taken as a Counter clockwise current to be positive. A circular conducting coil of radius 2R is placed in the equatorial plane of the solenoid and concentric with the solenoid itself. Then the current induced in the outer coil is correctly shown as a function of time by which of the following graph:
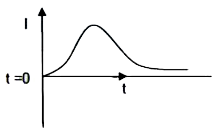


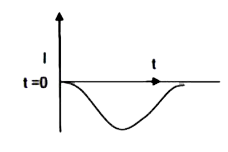
The correct Answer is:B

lind ∝−didt=−ddt(αte−βt)
=−(αe−βt+αte−βt(−β))
=−αe−βt(1−βt)
Check value of at t = 0
Topper's Solved these Questions
Similar Questions
A very long solenoid of radius R is carrying current I(t)=kte−αt , as a function of time (t≥0). Counter clockwise current is taken to be positive. A circular conducting coil of radius 2R is placed in the equatorial plane of the solenoid and concentric with the solenoid. the current induced inthe outer coil is correctly depicted, as function of time by :
View SolutionA small, conducting circular loop is placed inside a long solenoid carrying a current. The plane of the loop contains the axis of the solenoid. If the current in the solenoid is varied, the current induced in the loop is
View Solution
Knowledge Check
A small, conducting circular loop is placed inside a long solenoid carrying a current. The plane of the loop contains the axis of the solenoid. If the current in the solenoid is varied, the current induced in the loop is
AclockwiseBanti-clockwiseCzeroDclockwise or anti-clockwise depending on whether the resistance is increased or decreasedA long solenoid of radius R carries a time (t) – dependent current I=I0(t−2t2) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30∘ with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
A0.5B1.0 secC0.25 secD0.75 secA long solenoid of radius R carries a time (t) – dependent current I=I0(t−2t2) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30∘ with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
A0.5 secB1.0 secC0.25 secD0.75 sec
A small, conducting circular loop is placed inside a long solenoid carrying a current. The plane of the loop contains the axis of the solenoid. If the current in the solenoid is varied, the current induced in the loop is
View SolutionA long solenoid of radius R carries a time (t) – dependent current I=I0(t−2t2) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30∘ with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
View SolutionA long solenoid of radius R carries a time (t) – dependent current I=I0(t−2t2) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30∘ with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
View SolutionThe magneitc field produced at the center of a current carrying circular coil of radius r, is
View SolutionThe magnetic field produced at the center of a current carrying circular coil of radius r, is
View Solution
