A steady current I goes through a wire loop PQR having shape of a right angle triangle with PQ=3x,PR=4xandQR=5x. If the magnitude of the magnetic field at P due to this loop is k(μ0I48πx), find the value of K.
The correct Answer is:7
The magnetic field at P due to current elements PQ and PR is zero as the point P is on the conductor.
Therefore, the magnetic field at P due to current element QR is
B=μ0I4π(PD)[sinϕ1+sinϕ2]
=μ0I4π×12x⎡⎢
⎢⎣(9x5)3x+(16x5)4x⎤⎥
⎥⎦
=μ0I×548πx(35+45)
=748μ0Iπx
Topper's Solved these Questions
Similar Questions
A steady current I goes through a wire loop PQR having shape of a right angle triangle with PQ=3x,PR=4xandQR=5x. If the magnitude of the magnetic field at P due to this loop is k(μ0I48πx), find the value of K.
View SolutionA steady current I goes through a wire loop PQR having shape of a right angle triangle with PQ=3x,PR=4xandQR=5x. If the magnitude of the magnetic field at P due to this loop is k(μ0I48πx), find the value of K.
View Solution
Knowledge Check
A current /is flowing through the loop. The direction of the current and the shape of the loop are as shown in the figure. The magnetic field at the centre of the loop is μ0IR×(MA=R,MB=2R,∠DMA=90∘
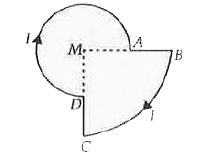 A516 ,but of the plane of the paper.B516, but into the plane of the paper.C716,but out of the plane of the paper.D716,but into the plane of the paper.
A516 ,but of the plane of the paper.B516, but into the plane of the paper.C716,but out of the plane of the paper.D716,but into the plane of the paper.A wire bent in the shape of a regular n-polygonal loop carries a steady current I. Let l be the perpendicular distance of a given segment and R be the distance of vertex both from the centre of the loop. The magnitude of the magnetic field at the centre of the loop is given by -
Anμ0I2πlsin(π/n)Bnμ0I2πRsin(π/n)Cnμ0I2πlcos(π/n)Dnμ0I2πRcos(π/n)
Figure shows a square loop ABCD with edge length a. The resistance of the wire ABC is r and that of ADC is 2r. Find the magnetic field B at the centre of the loop assuming uniform wires.

View SolutionIf the sides of a right angled triangle are 3,4 and 5m and a current of magnitude I is flowing in the direction as shown in the fig.If the magnitude of magnetic field at point "B" is kμd48π .Find the value of k.
View SolutionA square loop of wire, edge length a, carries a current i. Compute the magnitude of the magnetic field produced at a point on the axis of the loop at a distance x from the centre.
View SolutionA current loop, carrying a current of 5.0 A, is in the shape of a right triangle with sides 30,40, and 50 cm. The loop is in a uniform magnetic field of magnitude 80 mT whose direction is parallel to the current in the 50 cm side of the loop. Find the magnitude of (a) the magnetic dipole moment of the loop and (b) the torque on the loop.
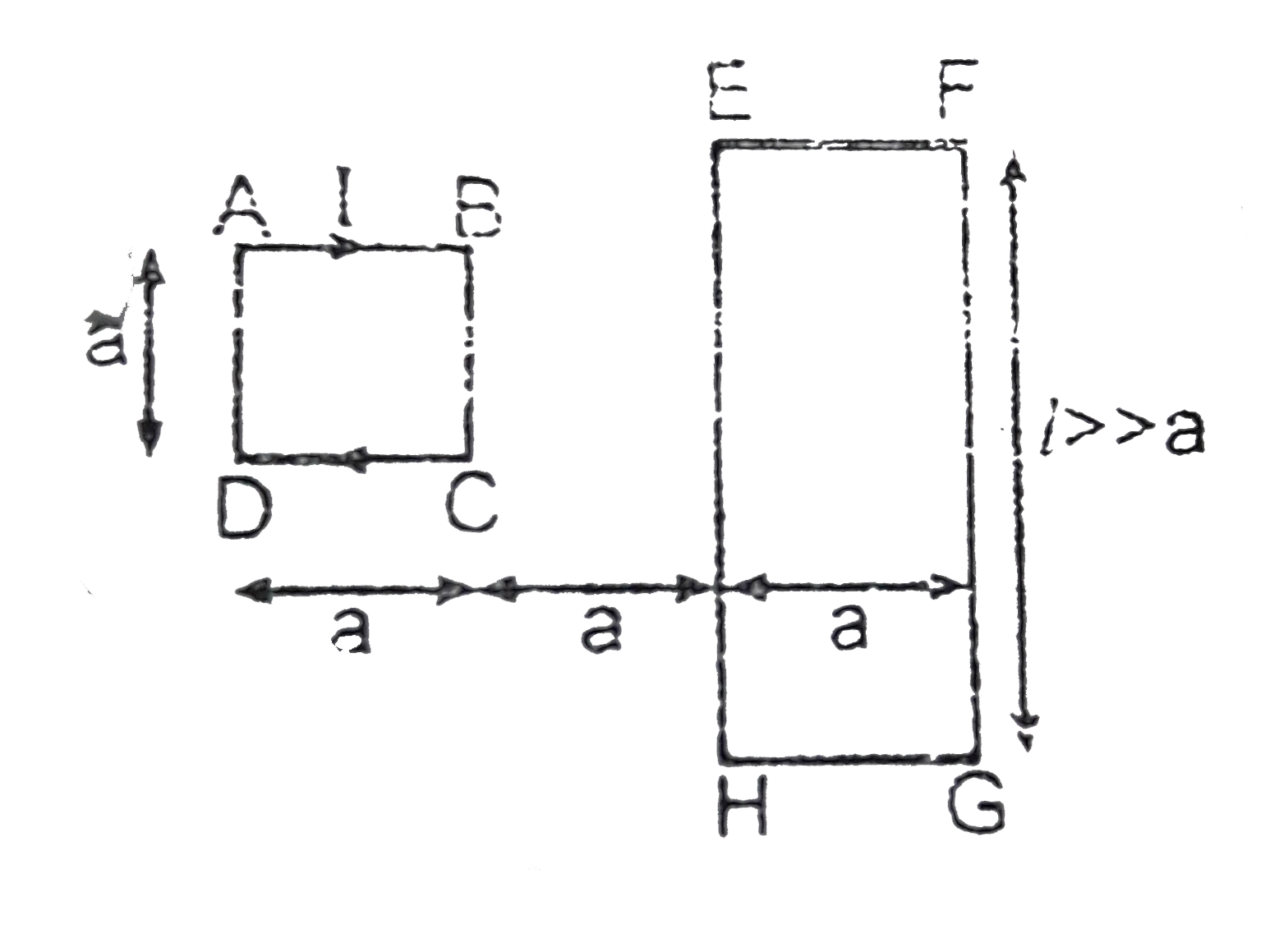
View SolutionIn the figure shown two loops ABCD & EFGH are in the same plane.The smaller loop carries time varying current I=bt, where b is a positive constant and t is time.The resistance of the smalller loop is r and that of the larger loop is R.:(Neglect the self inductance of large loop)
The magnetic force on the loop EFGH due to loop ABCD is μ20Iabxπ2Rln43.Findout value of x.
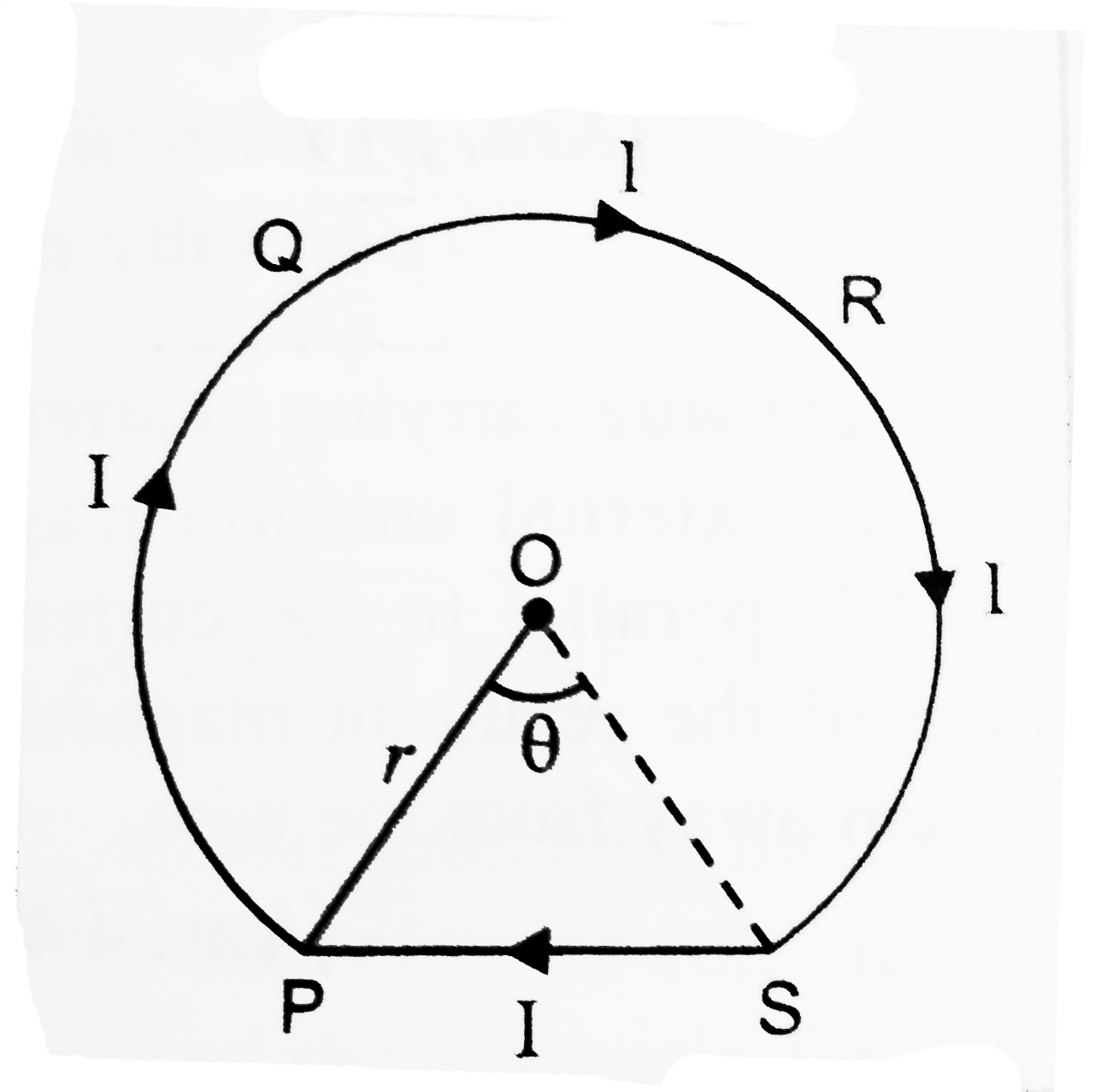
View SolutionA current I(=4A) flows along a thin wire PQRS shaped as shown in figure. The radius of the curved part of the wire is 10⋅0cm. The angle θ=90∘. Find the magnitude of the total magnetic field at the point O.
View Solution
