For the geometric series - 1−k+k2−k3+.....
Which of the following is false?
The series is convergent, if k=−13
The series is divergent, if k=-3
The series is oscillatory if k=-1
The series is divergent, if k=-2
The correct Answer is:C
Topper's Solved these Questions
Similar Questions
Knowledge Check
Let T(k) be the statement 1+3+5+…+(2k-1)=k2+10 Which of the following is correct ?
AT(1) is trueBT(k) is true ⇒ T (k+1) is trueCT(n) is true for all n∈NDAll above are correct
Let S(k)=1+3+5+...+(2k−1)=3+k2. Then which of the following is true ?
(A) S(1) is correct
(B) S(k)=S(k+1)
(C) S(k)≠S(k+1)
(D) Principal of mathematical induction can be used to prove the formula
View SolutionThe difference between the sum of the first k terms of the series 13+23+33+.......+n3 and the sum of the first k terms of 1+2+3+.......+n is 1980. The value of k is __________.
View SolutionThe difference between the sum of the first k terms of the series 13+23+33+....+n3 and the sum of the first k terms of 1+2+3+.....+n is 1980 . The value of k is :
View SolutionLet sk,k=1,2,3,…,100 denote the sum of the infinite geometric series whose first term is k−1⌊k and the common ratio is 1k. Then, the value of
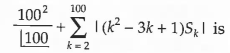 is
is
View SolutionLet Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
View SolutionLet Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
View SolutionLet Sk,k=1,2,….100 denote the sum of the infinite geometric series whose first term is k−1K! and the common
ration is 1k then the value of (100)2100!+Σ100k=1∣∣(k2−3k+1)Sk∣∣ is ____________
View Solution
