Each of these question have a questions followed by information given in three statements (1) (2) and (3). You have to study the question along with the information in three statements and decided that the information in which of the statement(s) is/are necessary to answer the question?
What is the area of the rectangular garden?
Perimeter of the garden is 220 metres
Length and the breadth of the garden are in the respective ratio of 7:4
Length is less than twice the breadth by 30 metres.
Only 1 and 2
Only 1 and 3
1 and either 2 or 3 only
Only 2 and 3
The correct Answer is:C
To determine the area of the rectangular garden, we need to analyze the information provided in the three statements.
Step 1: Understand the Question
We need to find the area of a rectangular garden. The area A of a rectangle is given by the formula:
A=Length×Breadth
Step 2: Analyze Statement (1)
Statement (1): Perimeter of the garden is 220 metres.
The perimeter P of a rectangle is given by the formula:
P=2(Length+Breadth)
From this statement, we can set up the equation:
2(L+B)=220
Dividing both sides by 2 gives:
L+B=110
This equation gives us a relationship between the length and breadth but does not provide their individual values.
Step 3: Analyze Statement (2)
Statement (2): Length and the breadth of the garden are in the respective ratio of 7:4.
Let’s express the length and breadth in terms of a variable x:
- Length L=7x
- Breadth B=4x
Now, substituting these into the equation from Statement (1):
7x+4x=110
11x=110
x=10
Now we can find the dimensions:
- Length L=7×10=70 metres
- Breadth B=4×10=40 metres
Step 4: Calculate the Area
Now we can calculate the area:
A=L×B=70×40=2800 square metres
Step 5: Analyze Statement (3)
Statement (3): Length is less than twice the breadth by 30 metres.
This can be expressed as:
L=2B−30
We already have L+B=110 from Statement (1). We can substitute L from this equation into the equation from Statement (3):
(2B−30)+B=110
3B−30=110
3B=140
B=1403
Now substituting back to find L:
L=2×1403−30=2803−30=280−903=1903
Now we can find the area:
A=L×B=(1903)×(1403)=266009 square metres
Conclusion
To find the area of the rectangular garden, we can conclude:
- Statement (1) is necessary to establish a relationship between length and breadth.
- Statement (2) is necessary to find the specific dimensions.
- Statement (3) is not necessary since we can find the area using Statements (1) and (2).
Final Answer
Thus, the necessary statements to answer the question are Statement (1) and Statement (2).
We need to find the area of a rectangular garden. The area A of a rectangle is given by the formula:
A=Length×Breadth
Statement (1): Perimeter of the garden is 220 metres.
P=2(Length+Breadth)
From this statement, we can set up the equation:
2(L+B)=220
Dividing both sides by 2 gives:
L+B=110
This equation gives us a relationship between the length and breadth but does not provide their individual values.
Statement (2): Length and the breadth of the garden are in the respective ratio of 7:4.
- Length L=7x
- Breadth B=4x
7x+4x=110
11x=110
x=10
- Length L=7×10=70 metres
- Breadth B=4×10=40 metres
Now we can calculate the area:
A=L×B=70×40=2800 square metres
Statement (3): Length is less than twice the breadth by 30 metres.
L=2B−30
(2B−30)+B=110
3B−30=110
3B=140
B=1403
Now substituting back to find L:
L=2×1403−30=2803−30=280−903=1903
A=L×B=(1903)×(1403)=266009 square metres
To find the area of the rectangular garden, we can conclude:
- Statement (1) is necessary to establish a relationship between length and breadth.
- Statement (2) is necessary to find the specific dimensions.
- Statement (3) is not necessary since we can find the area using Statements (1) and (2).
Thus, the necessary statements to answer the question are Statement (1) and Statement (2).
Topper's Solved these Questions
Similar Questions
Study the following graph carefully and answer the questions given below –
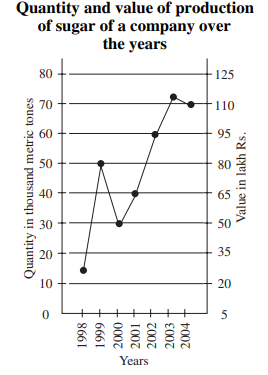
What was the difference between the average production of sugar during the average production of sugar during the year 1998, 1999, 2000 and 2001 and that of 2001, 2002, 2003 and 2004 in thousand metric tons?04:21View SolutionIn an election, one of the two candidates gets 40% votes and loses by 100 votes. Total number of votes is
03:27View SolutionEach of these questions consists of a question followed by informations in three statements. You have to study the question and the statements and decide that information in which of the statement(s) is/are necessary to answer the question.
What is the area of right angled trangle ?
(A) The perimeter of a triangle is 30 cm.
(B) The ratio between the base and the height of the triangle is 5:12.
(C ) The area of the triangle is equal to the area of a rectangle of length 10 cm.03:17View SolutionEach of these questions consists of a question followed by information in three statements I, II and III. You have to study the question and the statements and decide that the information in which of the statements(s) is/are required to answer the question.
Conclusions:
I. Some Colours are not Black
II. Some Hair can be Brown03:40View SolutionEach of these questions consists of a question followed by information in three statements I, II and III. You have to study the question and the statements and decide that the information in which of the statements(s) is/are required to answer the question. Conclusions: I. All Phones can be Calculators II. Some Phones are not Computers
05:17View SolutionEach of these questions consists of a question followed by information in three statements I, II and III. You have to study the question and the statements and decide that the information in which of the statements(s) is/are required to answer the question.
Conclusions:
I. Some Chalks are not Pencils
II. Some Chalks are not Pens05:15View SolutionEach of these questions consists of a question followed by information in three statements I, II and III. You have to study the question and the statements and decide that the information in which of the statements(s) is/are required to answer the question.
Conclusions:
I. Some Telegrams are not Postcards
II. All Telegrams can be LettersView SolutionEach of these questions consists of a question followed by information in three statements I, II and III. You have to study the question and the statements and decide that the information in which of the statements(s) is/are required to answer the question.
Conclusions:
I. Some Websites can never be Vlogs
II. Some Apps can be BlogsView SolutionIn each of the following questions a question is followed by information given in three statements. You have to study the question along with statements and decide the information given in which of the statement(s) is necessary and sufficient to answer the question.
What is the volume of the cylindrical tank?
Area of the base is x square metres
Height of the tank is y metres
Diameter of the base is equal to the height of the tank.05:34View SolutionIn each of the following questions a question is followed by information given in three statements. You have to study the question along with statements and decide the information given in which of the statement(s) is necessary and sufficient to answer the question.
How many children are three in the class?
20% children speak only Hindi
44 children can speak language other than Hindi
There are 30 boys in the class07:26View SolutionIn each of the following questions a question is followed by information given in three statements. You have to study the question along with statements and decide the information given in which of the statement(s) is necessary and sufficient to answer the question.
What is the speed of the train?
Length of the platform is 150% of the length of the train
The train crosses the platform in 25 seconds
The train crosses the signal pole in 10 seconds04:02View SolutionIn each of the following questions a question is followed by information given in three statements. You have to study the question along with statements and decide the information given in which of the statement(s) is necessary and sufficient to answer the question.
What is the selling price of the T.V. set if no discount is offered ?
Profit earned was 20%
Had 10% discount been offered on selling price the profit would have been Rs. 1200
Cost price is Rs. 15000View SolutionIn each of the following questions a question is followed by information given in three statements. You have to study the question along with statements and decide the information given in which of the statement(s) is necessary and sufficient to answer the question.
What is the average weight of girls in the class?
Average weight of all the 60 student is 42 kg
Average weight of boys is 43 kg
Total weight of all the girls together is 1144 kgView SolutionEach of these question have a questions followed by information given in three statements (1) (2) and (3). You have to study the question along with the information in three statements and decided that the information in which of the statement(s) is/are necessary to answer the question?
What is the principal amount?
Difference between simple interest and compound interest for 2 years is Rs. 37⋅50
Simple interest for 3 year is Rs.2⋅250
Simple interest and compound interest for the first year are equal04:43View SolutionEach of these question have a questions followed by information given in three statements (1) (2) and (3). You have to study the question along with the information in three statements and decided that the information in which of the statement(s) is/are necessary to answer the question?
What was the population of State ‘A’?
Males and females were in the ratio of 4:5 respectively
70% of the population was literate
8 lakh males were literate in the StateView Solution

