In the following figure, Q is a point on PR and S is a point on TR. QS is drawn and ∠RPT=∠RQS.
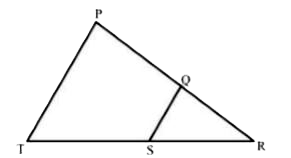
Which of these criteria can be used to prove that ΔRSQ is similar to ΔRTP?
AAA similarity criterion B
SAS similarity criterion
SSS similarity criterion
RHS similarity criterion
The correct Answer is:A
Step by step video, text & image solution for In the following figure, Q is a point on PR and S is a point on TR. QS is drawn and angleRPT= angleRQS. Which of these criteria can be used to prove that ΔRSQ is similar to DeltaRTP ? by Physics experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PRACTICE PAPER 2022BOOK - CBSE MODEL PAPERCHAPTER - PRACTICE PAPER 2022EXERCISE - Multiple Choice Questions
60 Videos
- CASE STUDY QUESTIONS CLASS 10TH EXAM 2020-21BOOK - CBSE MODEL PAPERCHAPTER - CASE STUDY QUESTIONS CLASS 10TH EXAM 2020-21EXERCISE - MCQs
239 Videos
- QUESTION BANK 2021BOOK - CBSE MODEL PAPERCHAPTER - QUESTION BANK 2021EXERCISE - QUESTIONS
60 Videos
Similar Questions
In Figure, T is a point on side QR of PQR and S is a point such that RT=ST. Prove That : PQ+PR>QS
View SolutionIn the following figures, PQ = LM, Q is the midpoint of PR and M is the midpoint of LN. Using the axioms, prove that PR = LN.

View SolutionIn the given figure, Q is a point on the side SR of ΔPSR such that PQ = PR. Prove that PS>PQ.
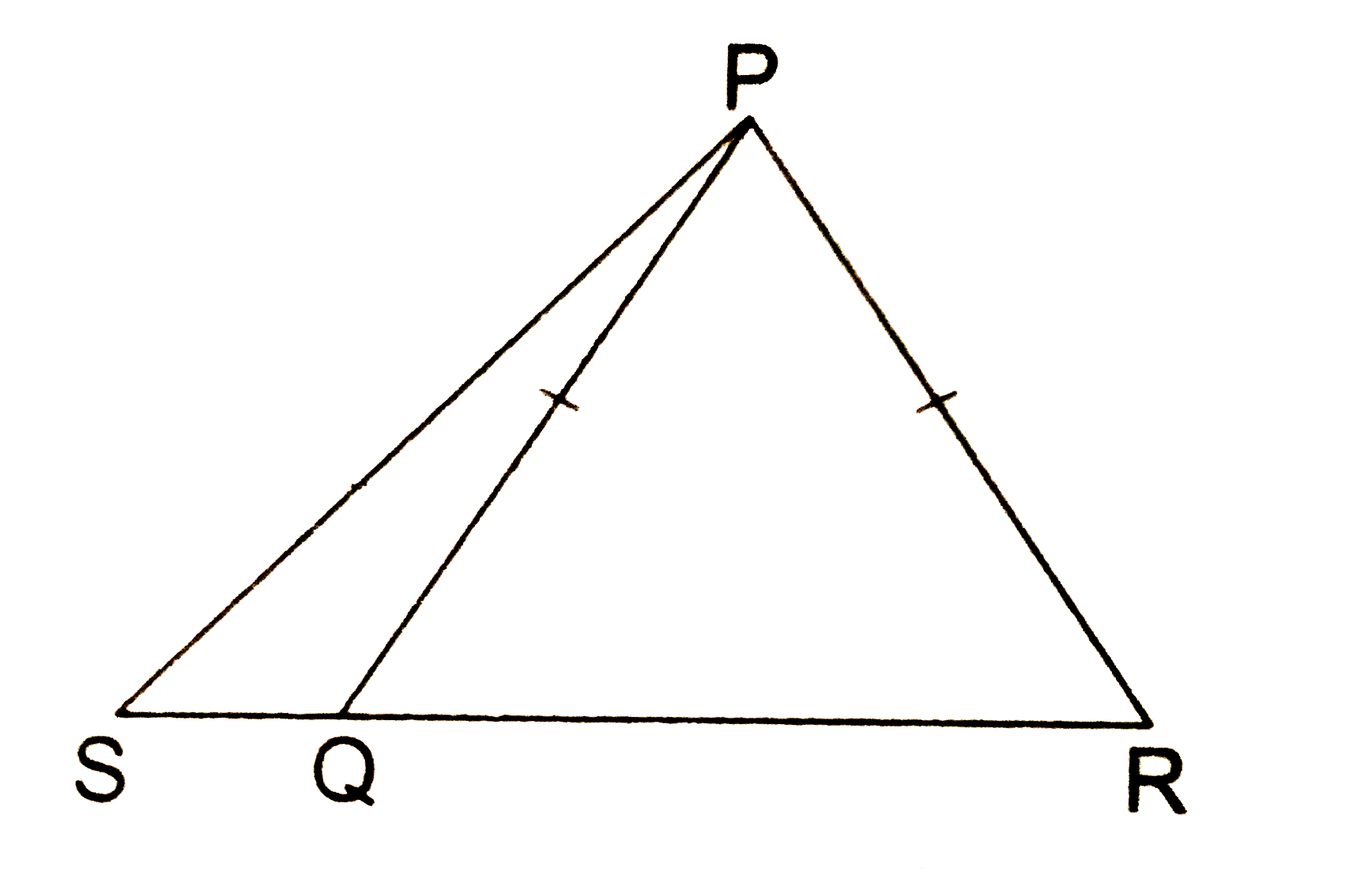
View SolutionIn ΔPQR,Pq=PR and S is the mid-point of PQ. A line drawn from S parallel to QR, intersects the line PR at T. Prove that PS = PT.
View SolutionIn the following figure, △PQR is right-angled at R and S is the mid-point of hypotenuse PQ. If RS=25cm and PR=48cm, then find QR.
View SolutionPQR is a triangle is which PQ=PR and S is any point on the side PQ . Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS=PT
In△PQR,wehavePQ=PR
View SolutionIn figure, PQR is a triangle in which PQ=PR and S is any point on the side PQ . Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS=PT.
View SolutionIn the figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R,S and P,Q respectively. Prove that : seg SQ ∣∣ seg RP.

View SolutionIn a triangle PQR, S and T are points on QR and PR respectively, such that QS=3SR and PT=4TR. Let M be the point of intersection of PS and QT. Determine the ratio QM:MT
View SolutionIn the given figure, P,Q,R and S are concylic points, and O is the mid-point of the diameter QS. If ∠QPR=25∘, then find ∠SQR.

View Solution
