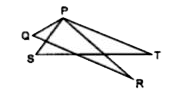
In the given if $Δ P Q R ~ Δ P S T and P T : S T = 3 : 4$ then QR : PR =

$3 : 4$

$4 : 3$

$3 : 7$

$4 : 7$

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

It is given that $Δ A B C ~ Δ P R Q and \frac{B C}{Q R} = \frac{2}{3} then \frac{a r (Δ P Q R)}{a r (Δ A B C)} = ?$
A $\frac{2}{3}$
B $\frac{3}{2}$
C $\frac{4}{9}$
D $\frac{9}{4}$
In $Δ D E F and Δ P Q R$ , if PQ =DE, EF=PR and FD =QR, then
A $Δ D E F ≅ Δ R P Q$
B $Δ D E F ≅ Δ Q P R$
C $Δ D E F ≅ Δ Q R P$
D $Δ D E F ≅ Δ P Q R$
In $Δ D E F and Δ P Q R$ , if PQ =DE, EF=PR and FD =QR, then
A $Δ D E F \equiv Δ R P Q$
B $Δ D E F \equiv Δ Q P R$
C $Δ D E F \equiv Δ Q R P$
D $Δ D E F \equiv Δ P Q R$