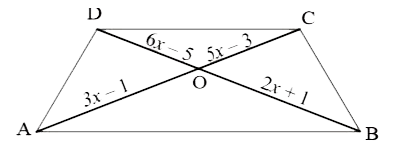
Amit went on a trip to Uttarakhand, India. While driving, he observes a bridge in the shape of a trapezium. Let AC and BD be the diagonals of the bridge, which intersect each other at a point O.

If OA=3x−1,OB=6x−5,OC=5x−3andOD=2x+1, then the value of x is :
A
1
B
2
C
4
D
6
Text Solution
The correct Answer is:B
|
Topper's Solved these Questions
- SIMILARITY BOOK - ICSECHAPTER - SIMILARITY EXERCISE - MULTIPLE CHOICE QUESTIONS (ASSERTION AND REASON BASED QUESTIONS)
5 Videos
- SHARES AND DIVIDENDSBOOK - ICSECHAPTER - SHARES AND DIVIDENDSEXERCISE - Exercise 3(C )
20 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(E)
61 Videos
Similar Questions
Knowledge Check
ABCD is a regular trapezium in which AD∣∣BC Diagonal AC and BD intersect at O, AO = 3 CO = X - 3 BO = 3X - 19 , DO = X - 5 . Find X
A−8,9B8,−9C−8,−9D8,9
The given figure shows a parallelogram ABCD whose diagonals intersect each other at point O. if OB=6 cm and AC is 6 cm more than BD, find OC.A12cmB10cmC9cmD11cmABCD is a trapezium in which AB parallel to DC and its diagonals intersect at P. If AP = (3x - 1) cm, PC = (5x - 3) cm, BP = (2x + 1) cm and PD = (6x - 5) cm, then the length of DB is:
ABCD एक समलम्ब है जिसमें AB, DC के समानांतर है तथा इसके विकर्ण P पर एक दूसरे को काठते हैं | यदि AP = (3x - 1) सेमी, PC = (5x - 3) सेमी, BP = (2x + 1) सेमी तथा PD = (6x - 5) सेमी है, तो DB की लंबाई क्या होगी ?A14 cmB12 cmC10 cmD16 cm
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O.
If AO = 2CO and BO = 2DO, show that:
OA×OD=OB×OC.
View Solution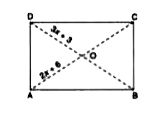
In the given figure, the diagonals AC and BD of a rectangle ABCD intersect each other at point O.
If OA=2x+6 and OD=3x+3, find the value of x.
View SolutionABCD is a trapezium such that AB||CD. Its diagonals AC and BC intersect each other at O. Prove that AOOC=BOOD
View SolutionABCD is a trapezium such that AB||CD. Its diagonals AC and BC intersect each other at O. Prove that AOOC=BOOD
View SolutionDiagonals AC and BD of a parallelogram ABCD intersect each other at O. If OA= 3 cm and OD = 2 cm, determine the lengths of AC and BD.
View Solution