In the following which of the two triangles are similar ?
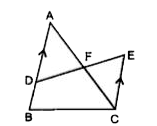
ΔADF~ΔCEF
ΔABC~ΔCEF
ΔADF~ΔABC
None of these
The correct Answer is:B
Topper's Solved these Questions
- SIMILARITY BOOK - ICSECHAPTER - SIMILARITY EXERCISE - MULTIPLE CHOICE QUESTIONS (ASSERTION AND REASON BASED QUESTIONS)
5 Videos
- SIMILARITY BOOK - ICSECHAPTER - SIMILARITY EXERCISE - MULTIPLE CHOICE QUESTIONS (COMPETENCY BASED QUESTIONS)
10 Videos
- SHARES AND DIVIDENDSBOOK - ICSECHAPTER - SHARES AND DIVIDENDSEXERCISE - Exercise 3(C )
20 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(E)
61 Videos
Similar Questions
Knowledge Check
Shown below are three triangles. The measures of two adjacent sides and included angle are given for each triangle.
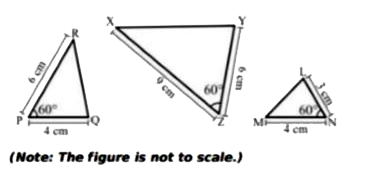
Which of these triangles are similar?AΔRPQandΔXZYBΔRPQandΔMNLCΔXZYandΔMNLDΔRPQ,andΔXZY are similar to one anotherIf the triangle ABC and DEF follows the given equation, then these two triangles are similar by which of the following criterion?
ABDE=BCEF=ACDFASAS similarityBAAA SimilarityCSSS SimilarityDNone of theseIf in triangles ABC and PQR, ABPQ=BCRP then write the equality of angles of the two triangles such that two triangles are similar.
A∠A=∠B∠B=∠PC∠C=∠QD∠B=∠Q
If in triangles ABC and PQR, ABPQ=ACRP then write the equality of angles triangles of the two triangles such that two triangles are similar.
View SolutionIf two angles of one triangle are respectively equal to two angles of another triangle; then two triangles are similar.
View SolutionSAS Similarity Criterion : If in two triangle; one pair of corresponding sides are proportional and the included angles are equal then two triangles are similar.
View SolutionConsider the following statements :
1. If two triangles are equiangular, then they are similar.
2. If two triangles have equal area, then they are similar.
Which of the statements given above is/are correct?
View SolutionIf in two triangles ABC and PQR, ABPQ=BCRP, then for the two triangles to be similar, which of the following condition is necessary?
View Solution
