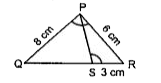
PQR is a triangle . S is a point on the QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm , then length of QR is …………..
12 cm
10 cm
8 cm
6 cm
The correct Answer is:A
Topper's Solved these Questions
- SIMILARITY BOOK - ICSECHAPTER - SIMILARITY EXERCISE - MULTIPLE CHOICE QUESTIONS (ASSERTION AND REASON BASED QUESTIONS)
5 Videos
- SIMILARITY BOOK - ICSECHAPTER - SIMILARITY EXERCISE - MULTIPLE CHOICE QUESTIONS (COMPETENCY BASED QUESTIONS)
10 Videos
- SHARES AND DIVIDENDSBOOK - ICSECHAPTER - SHARES AND DIVIDENDSEXERCISE - Exercise 3(C )
20 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(E)
61 Videos
Similar Questions
PQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

Find the lengths of QR and PS.
View SolutionPQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

Prove ΔPQR~ΔSPR.
View SolutionPQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

area of ΔPQRarea of ΔSPR
View SolutionIn ΔPQR,PQ=6√3cm,PR=12cmandQR=6cm then ∠Q is
View SolutionIn a triangle PQR, PQ = 20 cm and PR = 6 cm, the side QR is :
View SolutionIn ΔPQR, point S and T are on sides Pr and PQ such that ∠PQR=∠PST. If PT= 5 cm., PS = 3 cm. And TQ = 3 cm. then length of SR will be-
View SolutionIn ΔPQR, If ∠R=∠P, QR=4 cm and PR = 5 cm. Then, the length of PQ is
View SolutionIn ΔPQR, If angleR=angleP, QR=4 cm and PR = 5 cm. Then, the length of PQ is
View SolutionIn ΔPQR, S is a point in QR such that angle PQS= angle SPR show that angle PSR= angle QPR
View SolutionIn ΔPQR ∠R=∠P and QR=4cm and PR=5cm Then the length of PQ is
View Solution
