In an isosceles ΔABC right angled at B, then:
AB2=2AC2
AB2=AC2
AB2=AC24
AC2=2AB2
The correct Answer is:D
To solve the problem regarding the isosceles triangle ΔABC which is right-angled at B, we can follow these steps:
1. Understanding the Triangle:
We have an isosceles triangle ΔABC with a right angle at B. This means that AB=BC (the two sides opposite the equal angles).
2. Labeling the Sides:
Let AB=BC=x. Since ΔABC is right-angled at B, the hypotenuse AC will be opposite the right angle.
3. Applying the Pythagorean Theorem:
According to the Pythagorean theorem, in a right-angled triangle, the square of the hypotenuse AC is equal to the sum of the squares of the other two sides:
AC2=AB2+BC2
4. Substituting the Values:
Since AB=x and BC=x, we can substitute these values into the equation:
AC2=x2+x2
5. Simplifying the Equation:
This simplifies to:
AC2=2x2
6. Finding the Relationship:
We can express AC in terms of x:
AC=√2x2=x√2
Final Answer:
Thus, the relationship between the sides of the triangle is:
AC2=2⋅AB2
We have an isosceles triangle ΔABC with a right angle at B. This means that AB=BC (the two sides opposite the equal angles).
Let AB=BC=x. Since ΔABC is right-angled at B, the hypotenuse AC will be opposite the right angle.
According to the Pythagorean theorem, in a right-angled triangle, the square of the hypotenuse AC is equal to the sum of the squares of the other two sides:
AC2=AB2+BC2
Since AB=x and BC=x, we can substitute these values into the equation:
AC2=x2+x2
This simplifies to:
AC2=2x2
We can express AC in terms of x:
AC=√2x2=x√2
Thus, the relationship between the sides of the triangle is:
AC2=2⋅AB2
Topper's Solved these Questions
- SAMPLE PAPER 6BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section - A
6 Videos
- SAMPLE PAPER 6BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section - B
5 Videos
- SAMPLE PAPER 5BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - Section -C
2 Videos
- SAMPLE PAPER 7BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - Section -C
7 Videos
Similar Questions
Knowledge Check
If a ΔABC is right angled at B, then the diameter of the incircle of the triangle is
A2(c+ a - b)Bc+a - 2bCc + a- bDnone of theseP and Q are the mid-points of the sides AB and BC, respectively, of ΔABC, right angled at B. Then:
AAQ2+CP2=AC2BAQ2+CP2=45AC2CAQ2+CP2=43AC2DAQ2+CP2=54AC2In a ΔABC right angled at B, if the two legs AB and BC are in the ratio 1:3, evaluate the value of sin C.
A√103B3√10C13D1√10
ABC is a right isosceles triangle, right angled at B.
Then sin2A+cos2C= _________
View SolutionIn figure ABC is an isosceles triangle , right angled at C . Therefore
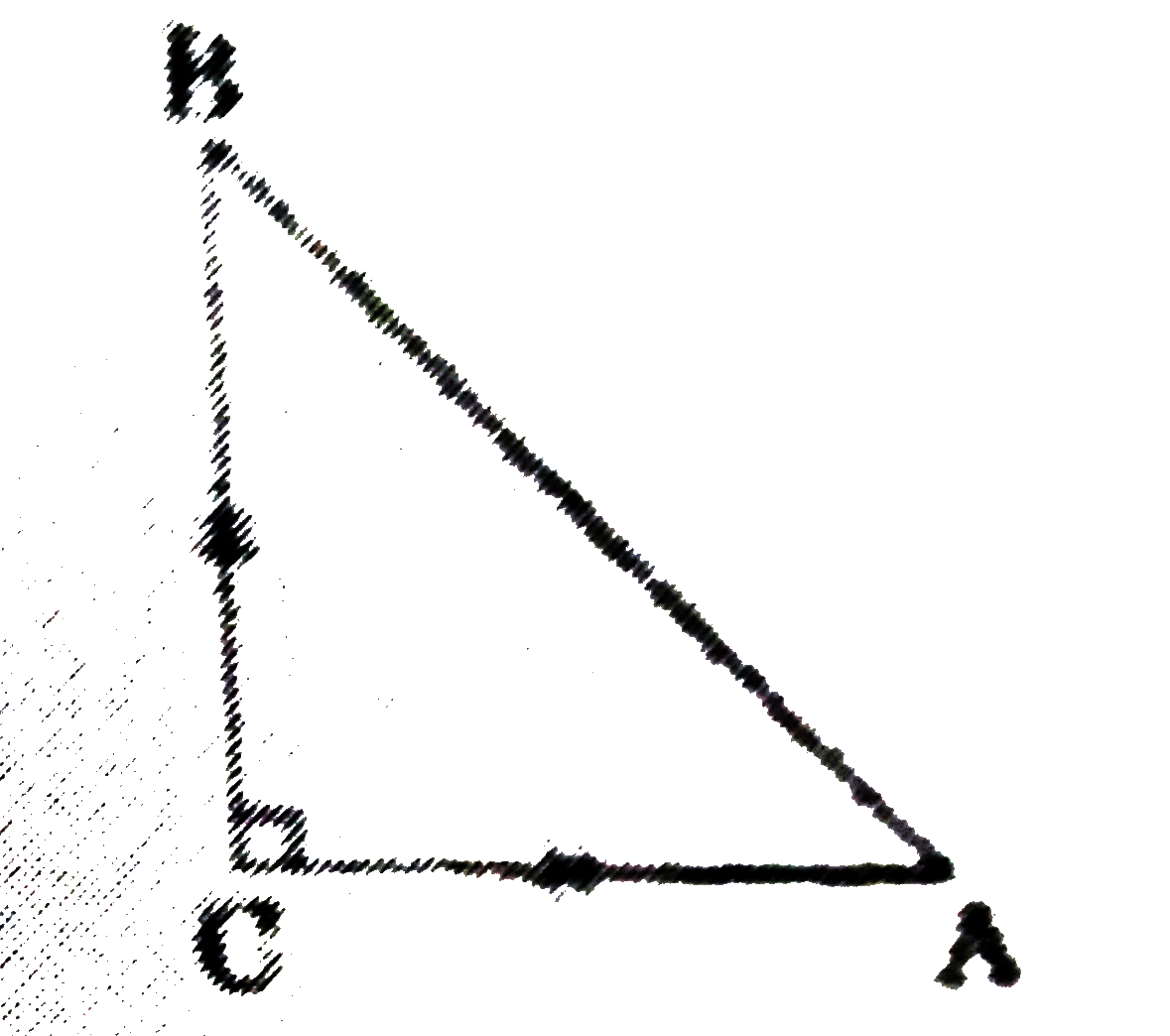
View SolutionIn a right angled ΔABC right angle at B if cosA=45 ,then what is sinC equal to?
View SolutionIn the given figure, ΔABC is right angled at B such that ∠BCA=2∠BAC. Show that hypotenuse AC = 2BC.
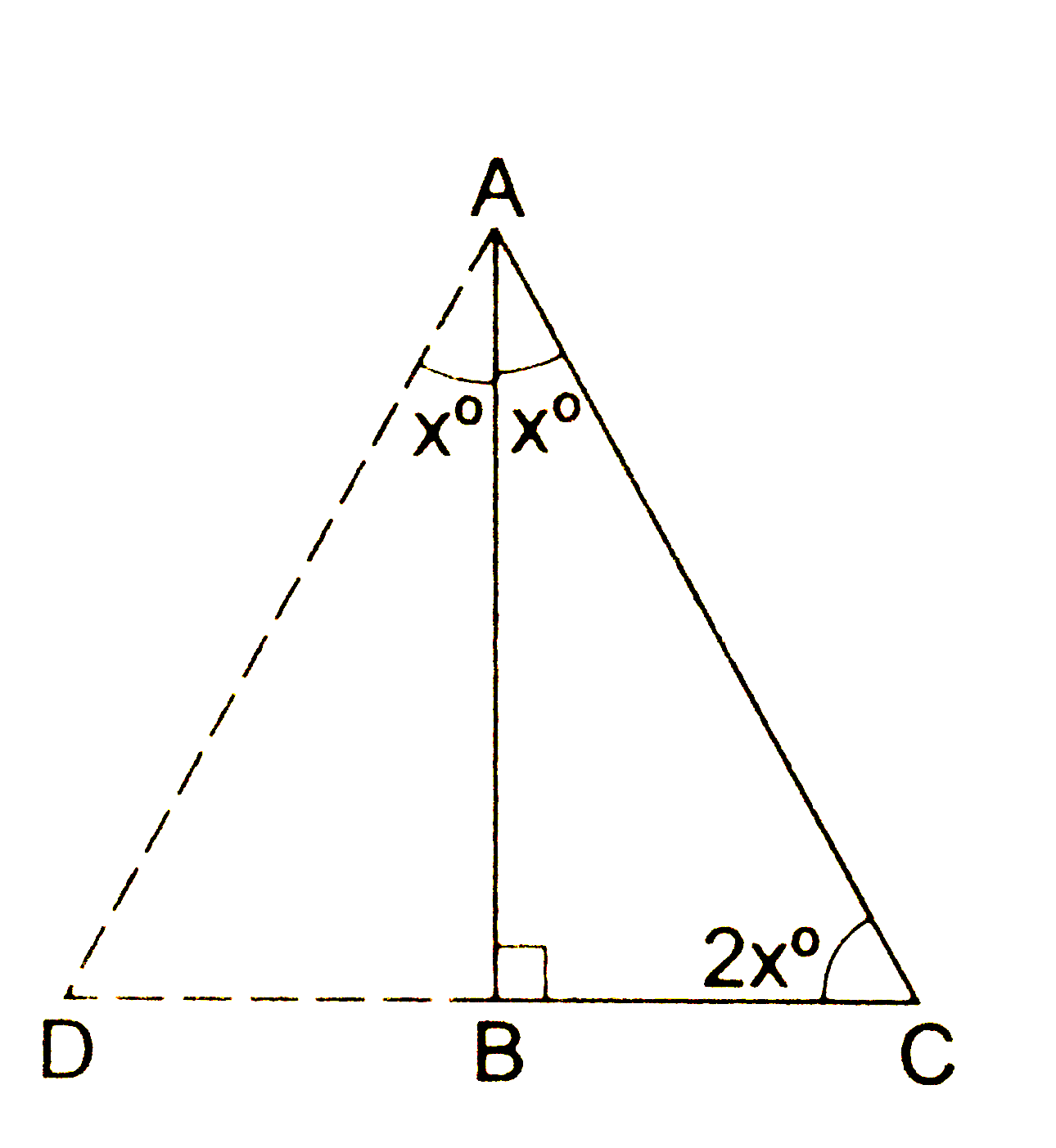
View SolutionIn an isosceles triangle ΔABC, if ∠B=70∘ find ∠A
View Solution
