The corner points of the feasible region for a linear programming problem are P(0,5), Q(1,5), R(4,2) and S(12,0). The minimum value of the objective function Z = 2x + 5y is the point
P
Q
R
S
To find the minimum value of the objective function Z=2x+5y at the given corner points of the feasible region, we will evaluate the function at each corner point.
1. Identify the corner points:
The corner points provided are:
- P(0,5)
- Q(1,5)
- R(4,2)
- S(12,0)
2. Substitute the coordinates into the objective function:
We will calculate Z for each point using the formula Z=2x+5y.
- For point P(0,5):
ZP=2(0)+5(5)=0+25=25
- For point Q(1,5):
ZQ=2(1)+5(5)=2+25=27
- For point R(4,2):
ZR=2(4)+5(2)=8+10=18
- For point S(12,0):
ZS=2(12)+5(0)=24+0=24
3. Compare the values of Z:
Now we summarize the values of Z at each point:
- ZP=25
- ZQ=27
- ZR=18
- ZS=24
4. Identify the minimum value:
The minimum value of Z occurs at point R(4,2) where Z=18.
Final Answer:
The minimum value of the objective function Z=2x+5y is at point R(4,2) with a value of 18.
---
The corner points provided are:
- P(0,5)
- Q(1,5)
- R(4,2)
- S(12,0)
We will calculate Z for each point using the formula Z=2x+5y.
ZP=2(0)+5(5)=0+25=25
ZQ=2(1)+5(5)=2+25=27
ZR=2(4)+5(2)=8+10=18
ZS=2(12)+5(0)=24+0=24
Now we summarize the values of Z at each point:
- ZP=25
- ZQ=27
- ZR=18
- ZS=24
The minimum value of Z occurs at point R(4,2) where Z=18.
The minimum value of the objective function Z=2x+5y is at point R(4,2) with a value of 18.
Topper's Solved these Questions
- QUESTION PAPER 2022 TERM 1 SET 1BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1EXERCISE - SECTION-C
10 Videos
- QUESTION PAPER 2022 TERM 1 SET 1BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1EXERCISE - SECTION-C
10 Videos
- EXAM REVISION SERIESBOOK - XII BOARDS PREVIOUS YEARCHAPTER - EXAM REVISION SERIESEXERCISE - All Questions
34 Videos
- QUESTION PAPER 2022 TERM 1 SET 2BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 1 SET 2EXERCISE - SECTION C
10 Videos
Similar Questions
The corner points of the feasible region of a system of linear inequalities are (0, 0), (4,0), (3,9), (1, 5) and (0, 3). If the maximum value of objective function, Z = ax + by occurs at points (3, 9) and (1, 5), then the relation between a and b is:
View SolutionThe corneer points of a feasible region, determined by a system of linear inequations, are (0,0),(1,0),(4,3),(2,1)and(0,1). If the objective function is Z=2x−3y, then the minimum value of Z is :
View Solution
Knowledge Check
The corner points of the feasible region of an LPP are (0,0),(0,8),(2,7),(5,4) and (6,0). The maximum value of the objective function Z = 3x + 2y is:
A20B23C27D18The corner points of the feasible region of a LPP are (20,0),(10,50),(0,60) and (0,0). If Z= 50x +15y, then maximum value of Z occurs at :
A(20,0)B(10,50)C(0.60)D(0,0)If the corner points of a feasible region of system of linear inequalities are (15,20) (40,15) and (2,72) and the objective function is Z = 6x + 3y then Zmax−Zmin =
A135B78C57D101
The corner points of a feasible region determined by a system of linear inequations are (0,0),(4,0),(5,2),(2,2) and (0, 1). If the objective function is Z = x + y, then maximum of Z occurs at:
View SolutionThe maximum value of objective function z=2x+3y in the given feasible region is
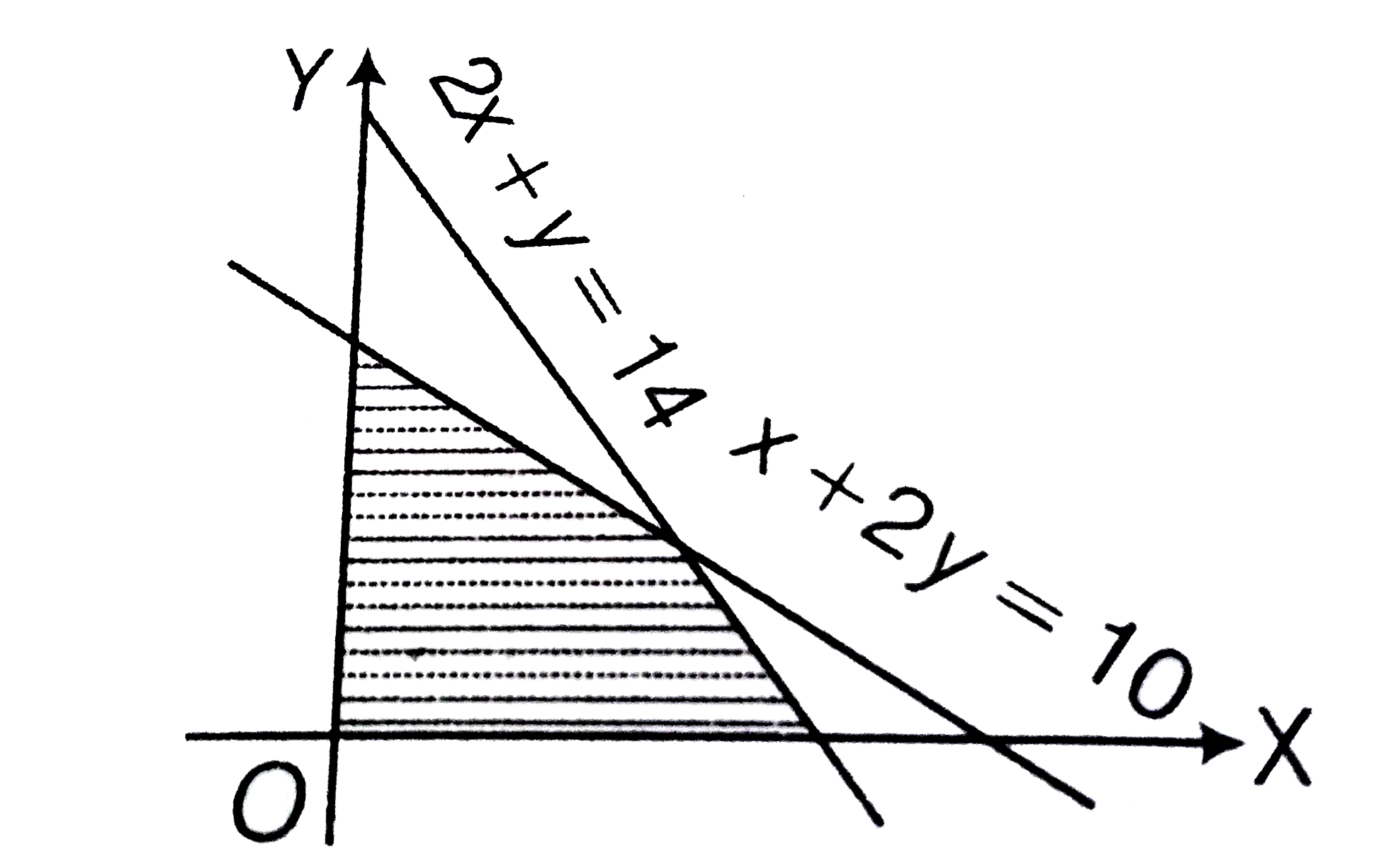
View SolutionThe corner points of a feasible region determined by a system of linear inequalities are (20,40),(50,100),(0,200) and (0,50). If the objective funtion Z=x+2y, then maximum of Z occurs at.
View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40). (20, 40), (60, 20). (60, 0). "The objective function is Z=4x+3y.
Compare the quantity in Column A and Column B.
Column AColumn BMaximum of Z325
View SolutionThe corner points of the feasible region determined by the system of linear contraints are (0,0), (0,40),( 20,40),(60,20),(60,0). The objective function is Z=4x+3y. Compare the quantity in Column A and Column B.
View Solution
