The magnitude of electric field due to a point charge 2q, at distance r is E. Then the magnitude of electric field due to a uniformly charged thin spherical shell of radius R with total charge q at a distance r2(r>>R) will be
E4
0
2E
4E
To solve the problem, we need to find the magnitude of the electric field due to a uniformly charged thin spherical shell of radius R with total charge q at a distance r2, given that r≫R.
Step 1: Understand the electric field due to a point charge
The electric field E due to a point charge Q at a distance r is given by the formula:
E=kQr2
where k is Coulomb's constant.
Step 2: Electric field due to the spherical shell
For a uniformly charged thin spherical shell, the electric field outside the shell (at a distance greater than its radius) behaves as if all the charge were concentrated at its center. Thus, for a spherical shell with total charge q and radius R, the electric field at a distance d from the center (where d>R) is given by:
Eshell=kqd2
Step 3: Calculate the electric field at r2
In our case, we need to find the electric field at a distance r2. Since r≫R, r2 is also much greater than R. Therefore, we can use the formula for the electric field due to the shell:
Eshell=kq(r2)2
Step 4: Simplify the expression
Substituting r2 into the equation, we get:
Eshell=kq(r2)2=kqr24=4kqr2
Step 5: Relate it to the electric field E
From the problem, we know that the electric field due to the point charge 2q at distance r is E:
E=k(2q)r2
Step 6: Find the relationship
Now, we can express Eshell in terms of E:
Eshell=4kqr2=2⋅2kqr2=2E
Conclusion
Thus, the magnitude of the electric field due to the uniformly charged thin spherical shell at a distance r2 is:
2E
The electric field E due to a point charge Q at a distance r is given by the formula:
E=kQr2
where k is Coulomb's constant.
For a uniformly charged thin spherical shell, the electric field outside the shell (at a distance greater than its radius) behaves as if all the charge were concentrated at its center. Thus, for a spherical shell with total charge q and radius R, the electric field at a distance d from the center (where d>R) is given by:
Eshell=kqd2
In our case, we need to find the electric field at a distance r2. Since r≫R, r2 is also much greater than R. Therefore, we can use the formula for the electric field due to the shell:
Eshell=kq(r2)2
Substituting r2 into the equation, we get:
Eshell=kq(r2)2=kqr24=4kqr2
From the problem, we know that the electric field due to the point charge 2q at distance r is E:
E=k(2q)r2
Now, we can express Eshell in terms of E:
Eshell=4kqr2=2⋅2kqr2=2E
Thus, the magnitude of the electric field due to the uniformly charged thin spherical shell at a distance r2 is:
2E
Topper's Solved these Questions
- BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1EXERCISE - SECTION-B24videos
QUESTION PAPER 2022 TERM 1 SET 1
- BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1EXERCISE - SECTION-C6videos
QUESTION PAPER 2022 TERM 1 SET 1
- BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 SET - 5EXERCISE - SECTION-C (CASE STUDY)5videos
QUESTION PAPER 2022 SET - 5
- BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 1 SET 2EXERCISE - SECTION C6videos
QUESTION PAPER 2022 TERM 1 SET 2
Similar Questions
Knowledge Check
- Question 1 - Select One
The electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
AQ4πε0r for points outside and Q4πε0R for points inside the shellBQ4πε0e for both points inside nad outside the shellCzero for points outside and Q4πε0r for points inside the shellDzero for both points inside and outside the shell - Question 2 - Select One
The electric field due to uniformly charged sphere of radius R as a function of the distance from its centre is represented graphically by
A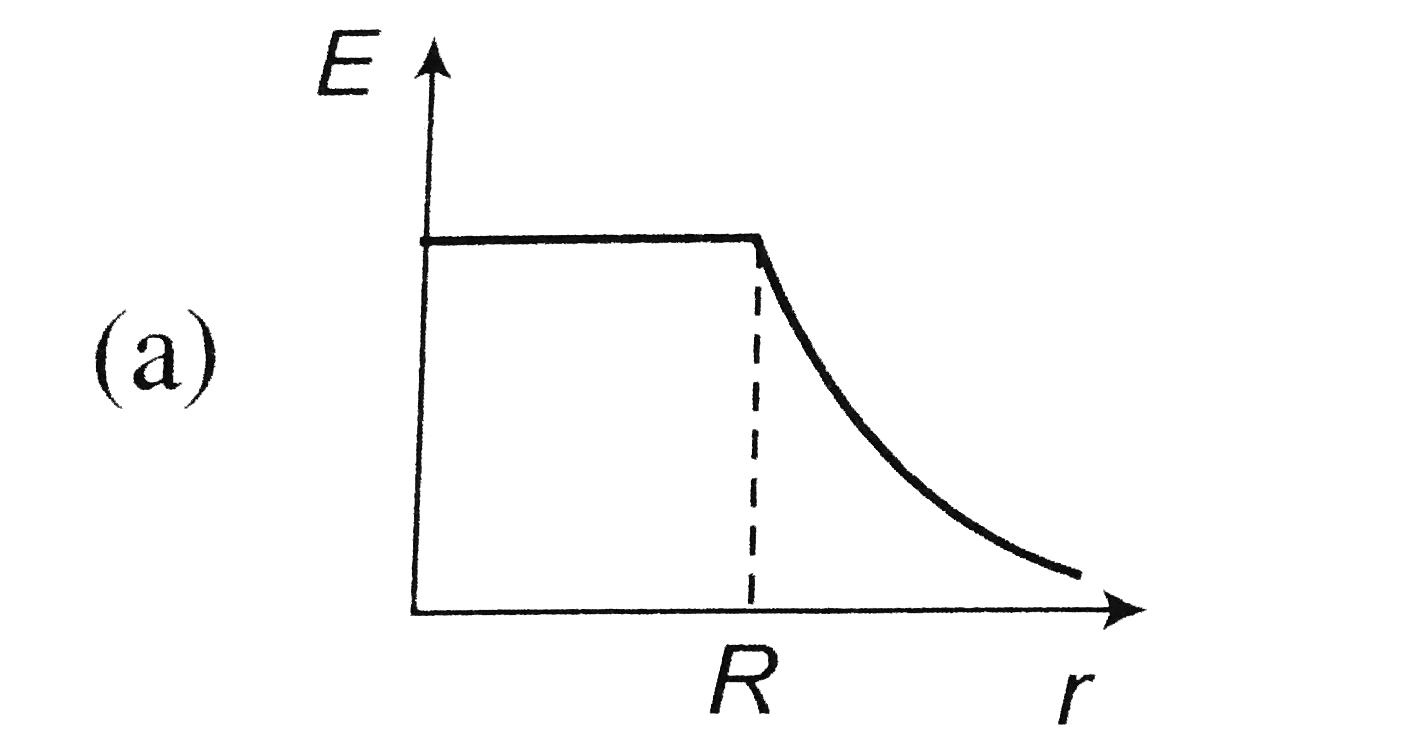 B
B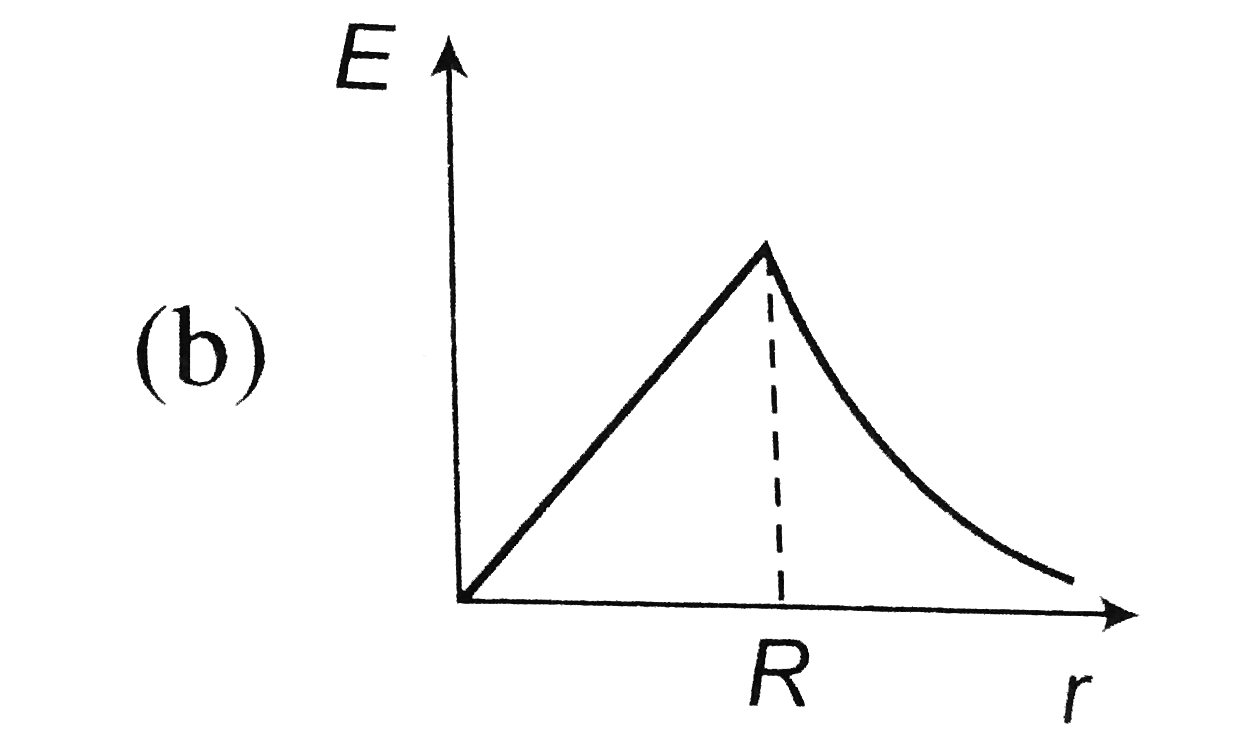 C
C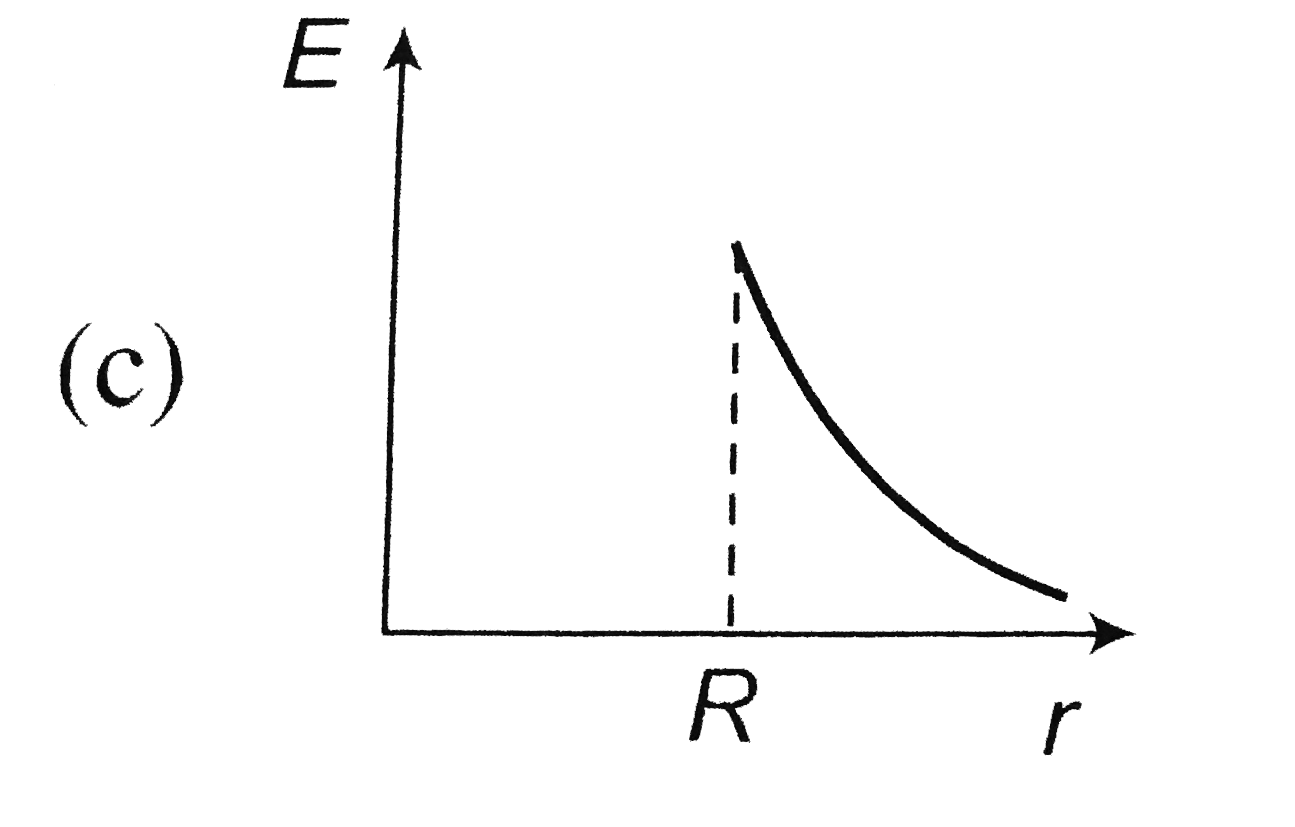 D
D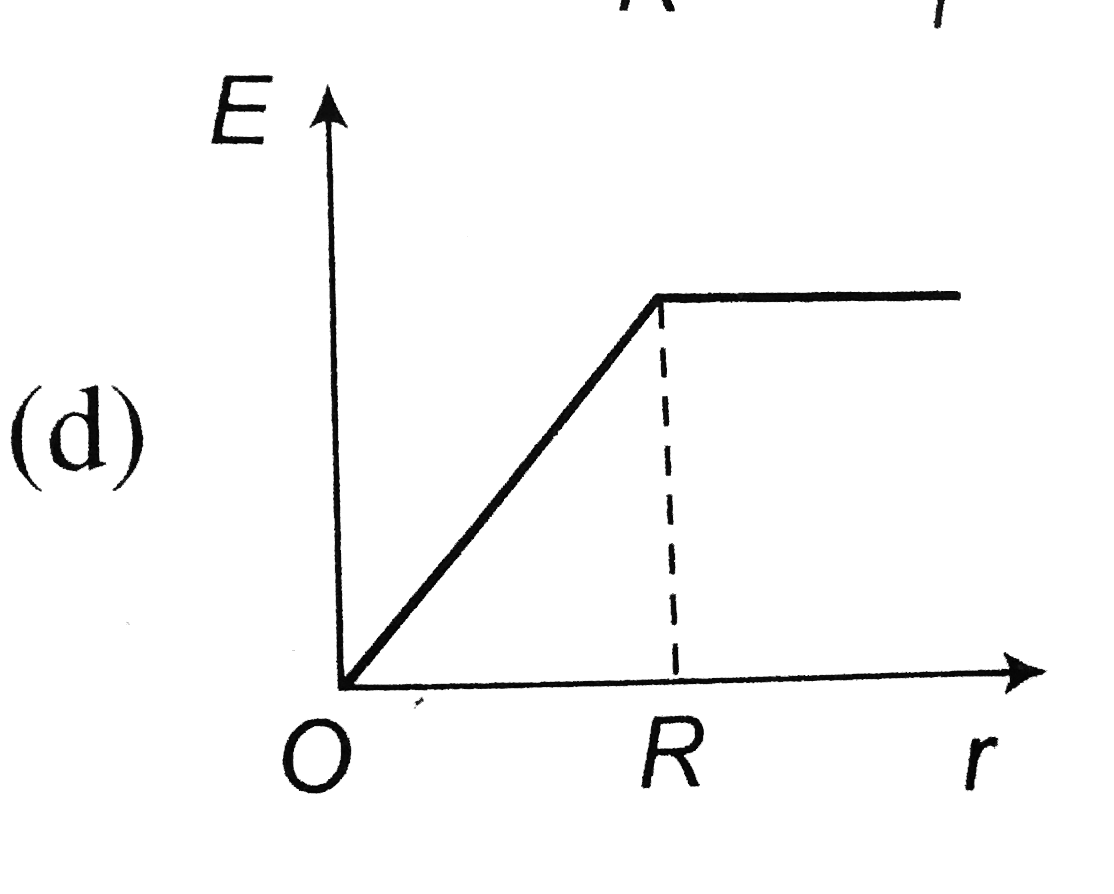
- Question 3 - Select One
Graphical representation of electric field due to uniformly charged sphere of radius R as function of distance from its centre is given by:
A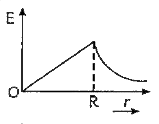 B
B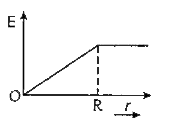 C
C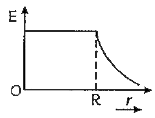 D
D
" Electric field intensity due to a point charge " "q" ' at a distance 'r' from it is "
View SolutionThe maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R will be
View SolutionThe electric intensity due to a uniformly charged infinite cylinder of radius R , at a distance r(>R) , from its axis is proportional to
View SolutionWhich of the following graph represents the variation of electric field E due to a thin charged spherical shell of radius R as a function of the distance r from the centre of the shell?
View SolutionThe electric field due to point charged at a distance R form it is E. if the same charge is placed on a metallic sphere of Radius R, the electric field on the surface of the sphere will be
View Solution

