A + 3.0 nC charge Q is initially at rest at a distance of r1=10 cm from a +5.0 nC charge q fixed at the origin . The charge Q is moved away from q to a new position at r2=15cm . In this process work done by the field is
1.29×10−5J
3.6×105J
−4.5×10−7J
4.5×10−7J
To find the work done by the electric field when moving a charge Q from an initial position r1 to a final position r2, we can use the formula for electric potential energy. The work done W by the electric field is equal to the change in electric potential energy ΔU of the charge Q.
1. Identify the Charges and Distances:
- Charge Q=3.0nC=3.0×10−9C
- Charge q=5.0nC=5.0×10−9C
- Initial distance r1=10cm=0.1m
- Final distance r2=15cm=0.15m
2. Calculate the Electric Potential Energy at Initial Position r1:
The electric potential energy U1 at distance r1 is given by:
U1=k⋅Q⋅qr1
where k=8.99×109N m2/C2 (Coulomb's constant).
Substituting the values:
U1=8.99×109⋅(3.0×10−9)⋅(5.0×10−9)0.1
U1=8.99×109⋅15.0×10−180.1
U1=8.99×109⋅1.5×10−17
U1=1.3485×10−7J
3. Calculate the Electric Potential Energy at Final Position r2:
The electric potential energy U2 at distance r2 is given by:
U2=k⋅Q⋅qr2
Substituting the values:
U2=8.99×109⋅(3.0×10−9)⋅(5.0×10−9)0.15
U2=8.99×109⋅15.0×10−180.15
U2=8.99×109⋅1.0×10−17
U2=8.99×10−8J
4. Calculate the Work Done by the Electric Field:
The work done W by the electric field is the change in potential energy:
W=U1−U2
W=1.3485×10−7−8.99×10−8
W=5.495×10−8J
Final Answer:
The work done by the electric field when moving the charge Q from r1 to r2 is approximately 5.495×10−8J.
- Charge Q=3.0nC=3.0×10−9C
- Charge q=5.0nC=5.0×10−9C
- Initial distance r1=10cm=0.1m
- Final distance r2=15cm=0.15m
The electric potential energy U1 at distance r1 is given by:
U1=k⋅Q⋅qr1
where k=8.99×109N m2/C2 (Coulomb's constant).
U1=8.99×109⋅(3.0×10−9)⋅(5.0×10−9)0.1
U1=8.99×109⋅15.0×10−180.1
U1=8.99×109⋅1.5×10−17
U1=1.3485×10−7J
The electric potential energy U2 at distance r2 is given by:
U2=k⋅Q⋅qr2
Substituting the values:
U2=8.99×109⋅(3.0×10−9)⋅(5.0×10−9)0.15
U2=8.99×109⋅15.0×10−180.15
U2=8.99×109⋅1.0×10−17
U2=8.99×10−8J
The work done W by the electric field is the change in potential energy:
W=U1−U2
W=1.3485×10−7−8.99×10−8
W=5.495×10−8J
The work done by the electric field when moving the charge Q from r1 to r2 is approximately 5.495×10−8J.
Topper's Solved these Questions
- QUESTION PAPER 2022 TERM 1 SET 1BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1EXERCISE - SECTION-C
6 Videos
- QUESTION PAPER 2022 TERM 1 SET 1BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1EXERCISE - SECTION-C
6 Videos
- QUESTION PAPER 2022 SET - 5BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 SET - 5EXERCISE - SECTION-C (CASE STUDY)
5 Videos
- QUESTION PAPER 2022 TERM 1 SET 2BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 1 SET 2EXERCISE - SECTION C
6 Videos
Similar Questions
Two charges q1=3.0μC and q2=−4.0μC initiallly are separated by a distance r0=2.0cm. An external agent moves the charges until they are rf=5.0cm apart.
(i) How much work is done by the electric field in moving the charges from r0 to rf ? Is the work positive or negative ?
(ii) How much work is donw by the external aganet in moving the charges from r0 to rf ? Is the work positive or negative ?
(iii) What is the positive energy of the initial state where the charge are r0=2.0 cm apart ?
(iv) What is the potential energy of the final state where the charges are rf=5.0cm apart ?
(v) What is the change in potential energy from the initial state to the final state ?
View SolutionA point charge q is placed at the origin . How does the electric field due to the charge very with distance r from the origin ?
View Solution
Knowledge Check
A point charge q1=−1.0μC is held stationary at the origin. A second point charge q2=+2.0μC moves from the point (1.0m,0,0) to (2.0m,0,0). How much work is done by the electric force on q2?
A9mJB−9mJC−18mJD18mJMagnitude of work done during the charging of a condenser from q=0 to q=Q is
AW=C2QBW=Q22CCW=√QCDW=QCTwo equal negative charges are fixed at points and on y-axis. A positive charge Q is released from rest at the point on the x-axis. The charge Q will:
Aexecute simple harmonic motion about the originBmove to the origin and remain at restCmove to infinityDsame as at point 25 cm aways form the surface
What work is required to bring a charge q=3.00μC originally a distance of 1.50 m from a charge Q=20.0μC until it is 0.50 m away ?
View SolutionA point charge q produces an electric field of magnitude 2NC−1 at a point distance 0.25 m from it. What is the value of charge ?
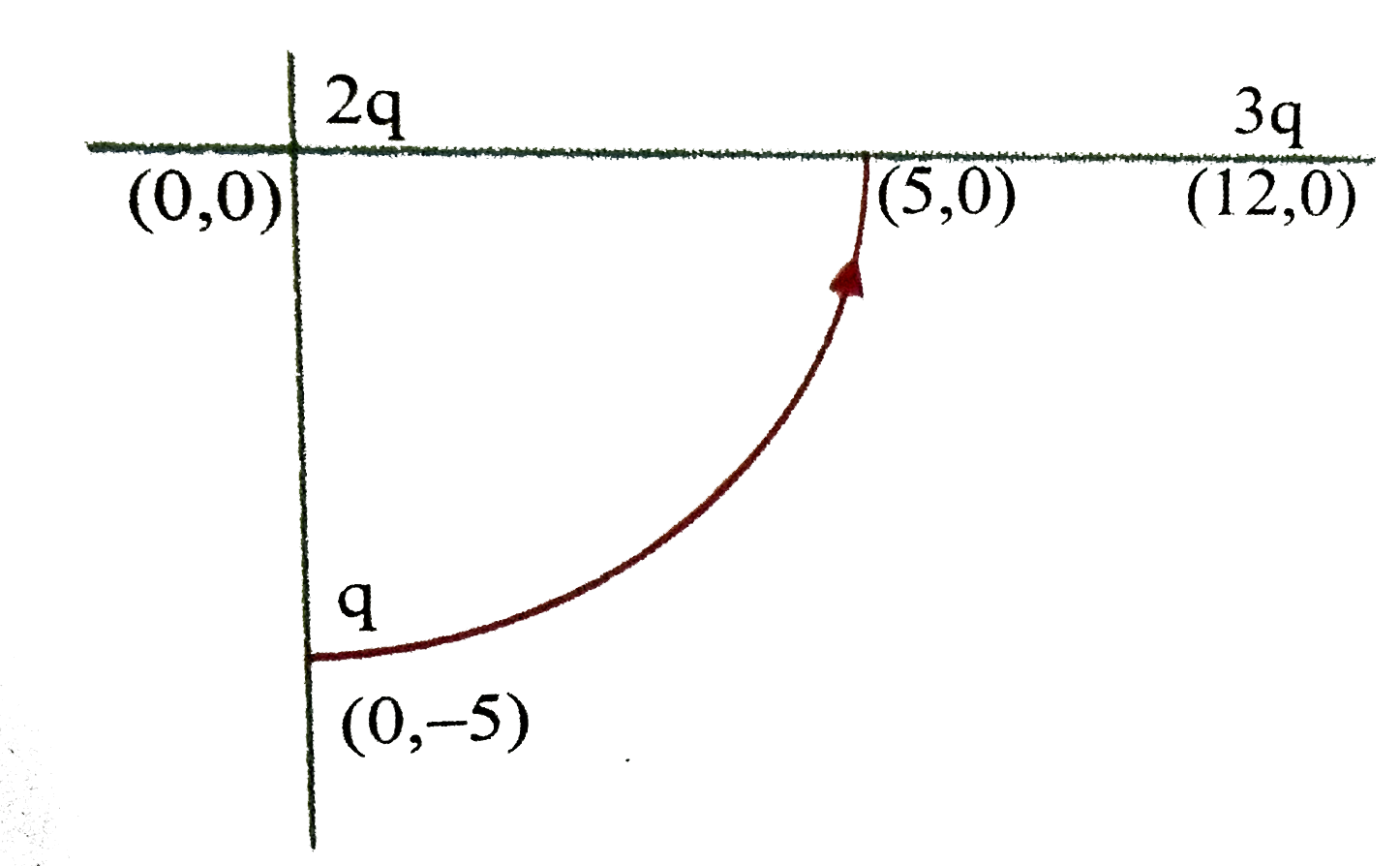
View Solution2q and 3q are two charges separated by a distance 12cm on x-axis .A third charge q is placed at 5cm on y−aξs as shown in figure .Find the change in potential energy of the system if 3q is moved from initial position to a point on X−aξs in circular path
View SolutionA particle of mass M and charge q , initially at rest , is accelerated by a uniform electric field E through a distance D and is then allowed to approach a fixed static charge Q of the same sign . The distance of the closest approach of the charge q will then be
View SolutionA fixed ring of radius R is given a charge q. A charge q0 is brought slowly from infinity to the centre of the ring. The wrong statement is-
View Solution
