A straight conducting rod of length l and mass m is suspended in a horizontal plane by a pair of flexible strings in a magnetic field of magnitude B. To remove the tension in the supporting strings, the magnitude of the current in the wire is .
mgBl
mglB
mglB
lBmg
To solve the problem, we need to find the magnitude of the current required to remove the tension in the supporting strings of a conducting rod suspended in a magnetic field.
1. Understanding the Forces Acting on the Rod:
- The rod has a mass m, which means it has a weight W=mg acting downwards, where g is the acceleration due to gravity.
- The rod is also subjected to a magnetic force when a current flows through it in the presence of a magnetic field B.
2. Magnetic Force on the Rod:
- When a current I flows through the rod of length l in a magnetic field B, the magnetic force Fm acting on the rod can be expressed as:
Fm=IlB
- This force acts in a direction perpendicular to both the current and the magnetic field.
3. Condition for Removing Tension:
- To remove the tension in the supporting strings, the upward magnetic force must balance the downward weight of the rod. Therefore, we set the magnetic force equal to the weight of the rod:
Fm=W
- Substituting the expressions for the forces, we have:
IlB=mg
4. Solving for Current I:
- Rearranging the equation to solve for the current I:
I=mglB
5. Final Expression:
- The magnitude of the current required to remove the tension in the strings is:
I=mglB
- The rod has a mass m, which means it has a weight W=mg acting downwards, where g is the acceleration due to gravity.
- The rod is also subjected to a magnetic force when a current flows through it in the presence of a magnetic field B.
- When a current I flows through the rod of length l in a magnetic field B, the magnetic force Fm acting on the rod can be expressed as:
Fm=IlB
- This force acts in a direction perpendicular to both the current and the magnetic field.
- To remove the tension in the supporting strings, the upward magnetic force must balance the downward weight of the rod. Therefore, we set the magnetic force equal to the weight of the rod:
Fm=W
- Substituting the expressions for the forces, we have:
IlB=mg
- Rearranging the equation to solve for the current I:
I=mglB
- The magnitude of the current required to remove the tension in the strings is:
I=mglB
Topper's Solved these Questions
- QUESTION PAPER 2022 TERM 1 SET 1BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1EXERCISE - SECTION-C
6 Videos
- QUESTION PAPER 2022 TERM 1 SET 1BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1EXERCISE - SECTION-C
6 Videos
- QUESTION PAPER 2022 SET - 5BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 SET - 5EXERCISE - SECTION-C (CASE STUDY)
5 Videos
- QUESTION PAPER 2022 TERM 1 SET 2BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 1 SET 2EXERCISE - SECTION C
6 Videos
Similar Questions
A straight conductor of length 60cm and mass 10gm is suspended horizontally by a pair of flexible leads in a magnetic field of 0.4T as shown in figure. A current at 0.41A should be passed through the conductor to just remove the tension in the supporting cable. The total tension in the leads if the direction of current is reversed is found 1.96×10−yN. Find y ?

View SolutionA wire of 60 cm length and mass 16 gm is suspended by a pair of flexible leads in a magnetic field of induction 0.40 T. What are the magnitude and direction of the current required to remove the tension in the supporting leads?

View Solution
Knowledge Check
A uniform rod of length 3L and mass m is suspended from a horizontal roof by two strings of length L and 2L as shown. Then the tension in the left string of length L is :
 AmgBmg4Cmg2Dmg3
AmgBmg4Cmg2Dmg3A uniform rod of length l and mass M is suspended on two vertical inextensible string as shown in figure. Then tension T in the left string at the instant, when right string snaps is?
 AT=MgBT=Mg2CT=Mg4DT=zero
AT=MgBT=Mg2CT=Mg4DT=zeroA conducting rod of 1 m length and 1 kg mass is suspended by two verticle wires through its ends. An external magnetic field of 2T is applied normal to the rod. Now the current to be passed through the rod so as to make the tension in the wire zero is
[Take g=10ms−2]A15 AB5AC1.5AD2.5A
A wire of 62.0cm length and 13.0g mass is suspended by a pair of flexible leads in a uniform magnetic field of magnitude 0.440T in figure. What are the magnitude and direction of the current required to remove the tension in the supporting leads? Take g=10ms2
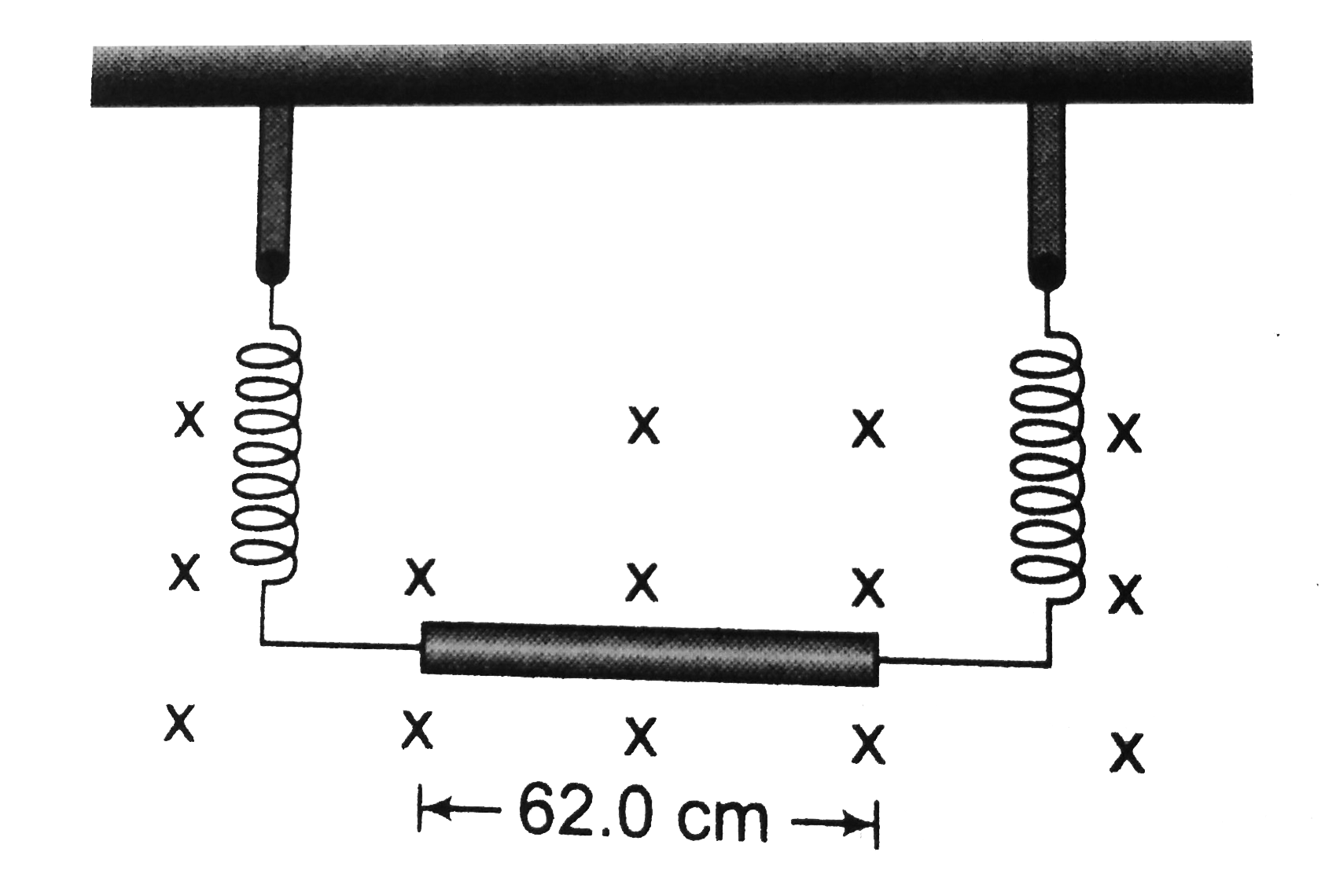
View SolutionA straight horizontal conducting rod of length l and mass m is suspended by two vertical wires at its ends. A current I is set up in the rod through the wires.
(i) What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero.
(ii) What will be the total tension in the wires if the direction of current is reversed, keeping the magnetic field same as before?
View SolutionA conducting rod of 1 m length and 1 kg mass is suspended by two vertical wires through its ends. An external magnetic field of 2T is applied normal to the rod. Now, the current to be passed through the rod so as to make the tension in the wires zero is : (Take g=10ms−2) :
View SolutionA straight wire of length L and carrying a curretn I stays suspended horizontally in mid air in a region where there is a uniform magnetic field →B. The linear mass density of the wire is λ. Obtain the magnitude and direction of this magnitude field.
View SolutionAn iron rod of mass 50 g and length 50 cm is suspended by master wires as shown in the figure. Calculate the magnitude and direction of magnetic field to be set in the region such that the tension is the wires is zero. The current in the rod is 4 A.

View Solution
