Which of the following options is INCORRECT?
An angle of 52.5∘ can be constructed.
A triangle ABC can be constructed in which AB = 5 cm, ∠A=45∘andBC+AC=5cm.
A triangle ABC can be constructed in which BC = 6 cm, ∠C=30∘andAC−AB=4cm.
A triangle ABC can be constructed in which ∠B=60∘,∠C=45∘andAB+BC+AC=12cm.
The correct Answer is:B
To determine which of the options is incorrect, we will analyze each statement one by one.
1. Statement A: "An angle of 52.5 degrees can be constructed."
- This statement is true. Any angle can be constructed using a compass and a straightedge, including 52.5 degrees. Therefore, this option is not incorrect.
Hint: Remember that any angle can be constructed with the right tools.
2. Statement B: "Triangle ABC can be constructed where AB = 5 cm, ∠A = 45°, and BC + AC = 5 cm."
- Here, we need to check the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
- Given that BC + AC = 5 cm, and AB = 5 cm, we can see that:
- BC + AC must be greater than AB (5 cm).
- However, since BC + AC = 5 cm, it does not satisfy the triangle inequality (it must be greater than 5 cm).
- Therefore, this statement is incorrect.
Hint: Recall the triangle inequality theorem when checking the feasibility of constructing a triangle.
3. Statement C: "Triangle ABC can be constructed where AB = 3 cm, ∠A = 30°, and BC + AC = 6 cm."
- For this statement, we check the triangle inequality again:
- BC + AC > AB (3 cm).
- Since BC + AC = 6 cm, this is greater than 3 cm, satisfying the condition.
- Therefore, this statement is true.
Hint: Ensure that the sum of any two sides is greater than the third side.
4. Statement D: "Triangle ABC can be constructed where AB = 4 cm, ∠A = 60°, and BC + AC = 8 cm."
- Again, we apply the triangle inequality:
- BC + AC must be greater than AB (4 cm).
- Since BC + AC = 8 cm, this is greater than 4 cm, satisfying the condition.
- Therefore, this statement is true.
Hint: Always check if the sum of two sides is greater than the third side.
Conclusion:
The incorrect option is B, as it violates the triangle inequality theorem.
- This statement is true. Any angle can be constructed using a compass and a straightedge, including 52.5 degrees. Therefore, this option is not incorrect.
- Here, we need to check the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
- Given that BC + AC = 5 cm, and AB = 5 cm, we can see that:
- BC + AC must be greater than AB (5 cm).
- However, since BC + AC = 5 cm, it does not satisfy the triangle inequality (it must be greater than 5 cm).
- Therefore, this statement is incorrect.
- For this statement, we check the triangle inequality again:
- BC + AC > AB (3 cm).
- Since BC + AC = 6 cm, this is greater than 3 cm, satisfying the condition.
- Therefore, this statement is true.
- Again, we apply the triangle inequality:
- BC + AC must be greater than AB (4 cm).
- Since BC + AC = 8 cm, this is greater than 4 cm, satisfying the condition.
- Therefore, this statement is true.
The incorrect option is B, as it violates the triangle inequality theorem.
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - CONSTRUCTIONSEXERCISE - Achievers Section (HOTS)5videos
CONSTRUCTIONS
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - CLASS 9 SAMPLE PAPER FINAL 4EXERCISE - MATHEMATICS10videos
CLASS 9 SAMPLE PAPER FINAL 4
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - COORDINATE GEOMETRY EXERCISE - ACHIEVERS SECTION (HOTS)2videos
COORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One

Which of the following combination is INCORRECT option ?A(i)(III)(R)B(III)(ii)(Q)C(III)(iv)(S)D(IV)(ii)(P) - Question 2 - Select One

Which of the following options is the only INCORRECT combination ?A(III) (iii) (R)B(III) (iv) (S)C(IV) (i) (R)D(I) (ii) (Q) - Question 3 - Select One
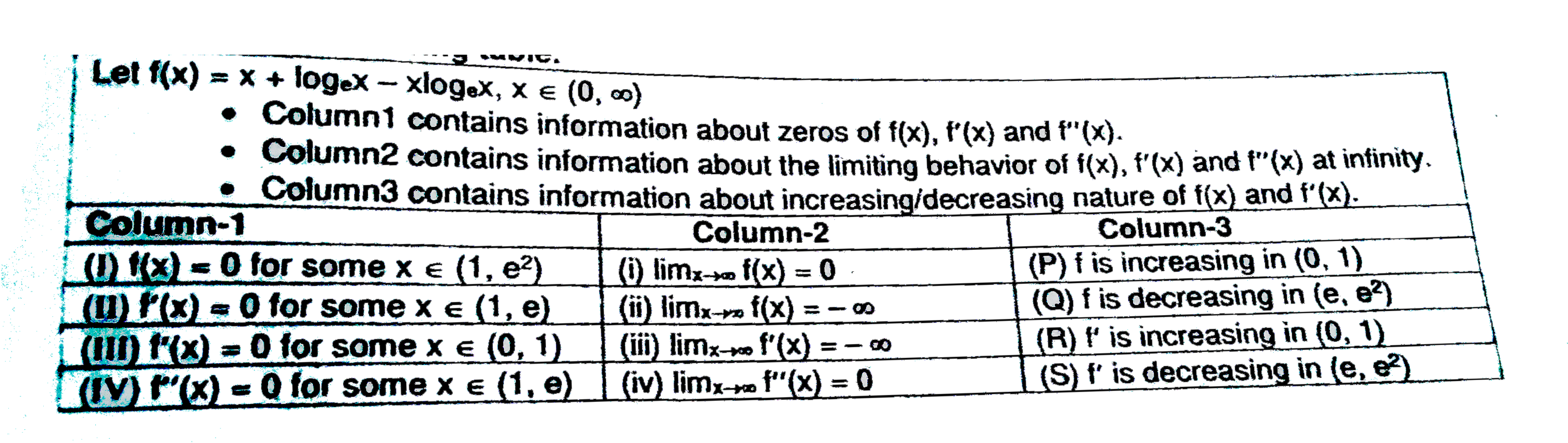
Which of the following options is the only INCORRECT combination ?A(I),(iii)(P)B(II)(iv)(Q)C(II),(iii)(P)D(III)(i)(R)


