Find the area of quadrilateral ABCD in which AB = 9 cm, BC = 40 cm, CD = 28 cm, DA = 15 cm and .
The correct Answer is:D
To find the area of quadrilateral ABCD, we can break it down into two triangles: triangle ABC and triangle ACD. Given that angle ABC is 90 degrees, we can easily calculate the area of triangle ABC using the formula for the area of a right triangle.
1. Identify the dimensions of triangle ABC:
- AB = 9 cm (base)
- BC = 40 cm (height)
2. Calculate the area of triangle ABC:
AreaABC=12×base×height=12×9×40
AreaABC=12×360=180 cm2
3. Use the Pythagorean theorem to find AC:
- AC is the hypotenuse of triangle ABC.
AC=√AB2+BC2=√92+402=√81+1600=√1681=41 cm
4. Identify the dimensions of triangle ACD:
- AD = 15 cm
- CD = 28 cm
- AC = 41 cm
5. Calculate the semi-perimeter (s) of triangle ACD:
s=AD+CD+AC2=15+28+412=842=42 cm
6. Use Heron's formula to find the area of triangle ACD:
AreaACD=√s(s−AD)(s−CD)(s−AC)
=√42(42−15)(42−28)(42−41)
=√42×27×14×1
=√42×27×14
To simplify:
42=14×3and27=9×3
=√(14×14)×(3×3)×1=√196×9=14×3=42 cm2
7. Calculate the total area of quadrilateral ABCD:
AreaABCD=AreaABC+AreaACD=180+42=222 cm2
Final Result:
The area of quadrilateral ABCD is 222 cm².
- AB = 9 cm (base)
- BC = 40 cm (height)
AreaABC=12×base×height=12×9×40
AreaABC=12×360=180 cm2
- AC is the hypotenuse of triangle ABC.
AC=√AB2+BC2=√92+402=√81+1600=√1681=41 cm
- AD = 15 cm
- CD = 28 cm
- AC = 41 cm
s=AD+CD+AC2=15+28+412=842=42 cm
AreaACD=√s(s−AD)(s−CD)(s−AC)
=√42(42−15)(42−28)(42−41)
=√42×27×14×1
=√42×27×14
42=14×3and27=9×3
=√(14×14)×(3×3)×1=√196×9=14×3=42 cm2
AreaABCD=AreaABC+AreaACD=180+42=222 cm2
The area of quadrilateral ABCD is 222 cm².
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - HERON'S FORMULAEXERCISE - Everyday Mathematics3videos
HERON'S FORMULA
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - COORDINATE GEOMETRY EXERCISE - ACHIEVERS SECTION (HOTS)2videos
COORDINATE GEOMETRY
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2016 SET A EXERCISE - Achievers Section5videos
IMO QUESTION PAPER 2016 SET A
Similar Questions
Knowledge Check
- Question 1 - Select One
A park is in the shape of quadrilateral ABCD in which AB=9cm,BC=12cm,CD=5cm,AD=8cm and ∠C=90∘. Find the area of the park.
A65.4cm2B69.4cm2C66.4cm2D68.4cm2 - Question 2 - Select One
The base of a right prism is a quadrilateral ABCD. Given that AB = 9 cm, BC = 14 cm, CD = 13 cm, DA = 12 cm and ∠DAB=90∘. If the volume of the prism be 2070cm3, then the area of the lateral surface is
A720cm2B810cm2C1260cm2D2070cm2
Find the area of a quadrilateral ABCD in which AB=3 cm, BC=4 cm, CD=4 cm, DA=5 cm and AC=5 cm.
View SolutionFind the area of a quadrilateral ABCD is which AB=3cm, BC=4cm, CD=4cm, DA=5cm and AC=5cm
S=12(a+b+c)=12(3+4+5)=6
arof ABC=sqrt(s(s-a)(s-b)(s-c)<br>ar ABC=√6(6−3)(6−4)(6−5)
⇒√6×3×2×1=6cm2
Now in △ADC,S=a+b+c2
⇒s=5+4+52=142=7cm
By using Heron’s formula
Area of △ADC=√s(s−a)(s−b)(s−c)
=√7(7−5)(7−4)(7−5)
=√7×2×3×2
=2√21cm2
Area of△ADC=9.2cm2 (approx.)
Area of the quadrilateral ABCD = Area of △ADC+Areaof△ABC=9.2cm2+6cm2=15.2cm2
Thus, the area of the quadrilateral,ABCDis15.2cm2.View SolutionFind the area of the quadrilateral ABCD in which AB = 9 m, BC = 40 m, ∠ABC=90∘, CD = 15 m and AD = 28 m.
View SolutionFind the area of the quadrilateral ABCD in which AB=3cm,BC=4cm,CD=4cm,DA=5cm and AC=5cm.
View SolutionFind the area of the quadrilateral ABCD; in which AB = 7 cm; BC =6 cm;CD =12 cm; DA= 15 cm and AC =9 cm
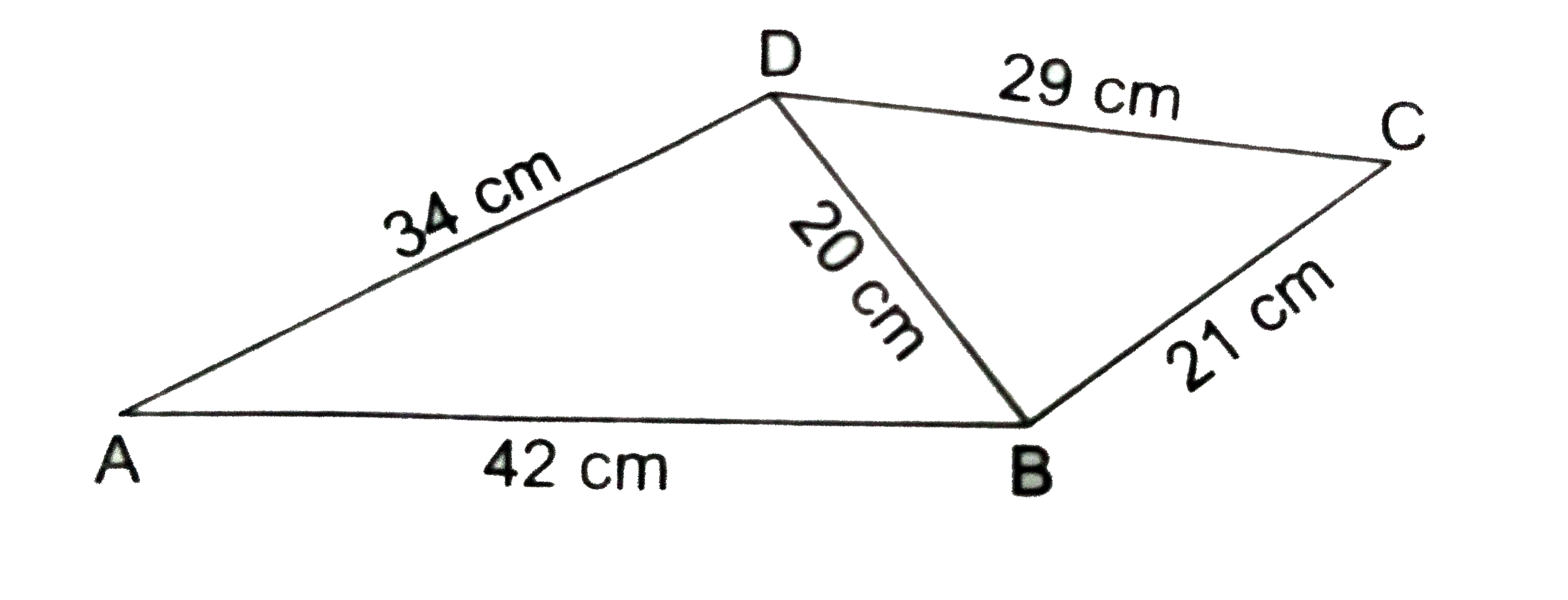
View SolutionFind the area of the quadrilateral ABCD in which AB= 42 cm. Bc=21cm,CD=29cm,DA=34cmand diagonal BD= 20 cm .
 View Solution
View Solution

