State 'T' for true and 'F' for false.
(I) The lengths of the three sides of a triangular field are 40 m, 24 m and 32 m respectively. The area of the triangle is 384 m2.
(II) The area of a quadrilateral ABCD in which AB=3 cm, BC=4 cm, CD=4 cm, DA = 5 cm and AC = 5 cm is 18 cm2.
(III) An advertisement board is in the form of an isosceles triangle with its sides equal to 12 m, 10 m and 10 m. The cost of painting it at Rs 2.25 per m2 is Rs 112.
(IV) Heron's formula cannot be used to calculate area of quadrilaterals.
IIIIIIIVTFFT
IIIIIIIVFTFF
IIIIIIIVTFTF
IIIIIIIVTFFF
The correct Answer is:D
To solve the given statements, we will analyze each one step by step using Heron's formula and other relevant geometric principles.
Statement (I):
The lengths of the three sides of a triangular field are 40 m, 24 m, and 32 m respectively. The area of the triangle is 384 m².
Step 1: Calculate the semi-perimeter (s) of the triangle.
s=A+B+C2=40+24+322=962=48 m
Step 2: Use Heron's formula to find the area (A) of the triangle.
A=√s(s−A)(s−B)(s−C)=√48(48−40)(48−24)(48−32)
=√48×8×24×16
Step 3: Calculate the values inside the square root.
=√48×8×24×16=√48×8×384=√147456
Step 4: Simplify the square root.
=384 m2
Conclusion for Statement (I): The statement is True (T).
---
Statement (II):
The area of a quadrilateral ABCD in which AB=3 cm, BC=4 cm, CD=4 cm, DA=5 cm, and AC=5 cm is 18 cm².
Step 1: Divide the quadrilateral into two triangles by diagonal AC.
- Triangle ABC with sides AB = 3 cm, BC = 4 cm, AC = 5 cm.
- Triangle ACD with sides AD = 5 cm, CD = 4 cm, AC = 5 cm.
Step 2: Calculate the area of triangle ABC using Heron's formula.
sABC=3+4+52=6 cm
AABC=√sABC(sABC−3)(sABC−4)(sABC−5)=√6(6−3)(6−4)(6−5)=√6×3×2×1=√36=6 cm2
Step 3: Calculate the area of triangle ACD using Heron's formula.
sACD=5+4+52=7 cm
AACD=√sACD(sACD−5)(sACD−4)(sACD−5)=√7(7−5)(7−4)(7−5)=√7×2×3×2=√84≈9.165 cm2
Step 4: Total area of quadrilateral ABCD.
AABCD=AABC+AACD=6+9.165≈15.165 cm2
Conclusion for Statement (II): The statement is False (F).
---
Statement (III):
An advertisement board is in the form of an isosceles triangle with its sides equal to 12 m, 10 m, and 10 m. The cost of painting it at Rs 2.25 per m² is Rs 112.
Step 1: Calculate the semi-perimeter (s) of the triangle.
s=10+10+122=16 m
Step 2: Use Heron's formula to find the area (A) of the triangle.
A=√s(s−10)(s−10)(s−12)=√16(16−10)(16−10)(16−12)=√16×6×6×4
=√384≈19.6 m2
Step 3: Calculate the cost of painting.
Cost=Area×Cost per m2=19.6×2.25≈44.1 Rs
Conclusion for Statement (III): The statement is False (F).
---
Statement (IV):
Heron's formula cannot be used to calculate the area of quadrilaterals.
Conclusion for Statement (IV): This statement is False (F). Heron's formula can be used to find the area of quadrilaterals by dividing them into triangles.
---
Final Answers:
1. (I) T
2. (II) F
3. (III) F
4. (IV) F
---
The lengths of the three sides of a triangular field are 40 m, 24 m, and 32 m respectively. The area of the triangle is 384 m².
s=A+B+C2=40+24+322=962=48 m
A=√s(s−A)(s−B)(s−C)=√48(48−40)(48−24)(48−32)
=√48×8×24×16
=√48×8×24×16=√48×8×384=√147456
=384 m2
The area of a quadrilateral ABCD in which AB=3 cm, BC=4 cm, CD=4 cm, DA=5 cm, and AC=5 cm is 18 cm².
- Triangle ABC with sides AB = 3 cm, BC = 4 cm, AC = 5 cm.
- Triangle ACD with sides AD = 5 cm, CD = 4 cm, AC = 5 cm.
sABC=3+4+52=6 cm
AABC=√sABC(sABC−3)(sABC−4)(sABC−5)=√6(6−3)(6−4)(6−5)=√6×3×2×1=√36=6 cm2
sACD=5+4+52=7 cm
AACD=√sACD(sACD−5)(sACD−4)(sACD−5)=√7(7−5)(7−4)(7−5)=√7×2×3×2=√84≈9.165 cm2
AABCD=AABC+AACD=6+9.165≈15.165 cm2
An advertisement board is in the form of an isosceles triangle with its sides equal to 12 m, 10 m, and 10 m. The cost of painting it at Rs 2.25 per m² is Rs 112.
s=10+10+122=16 m
A=√s(s−10)(s−10)(s−12)=√16(16−10)(16−10)(16−12)=√16×6×6×4
=√384≈19.6 m2
Cost=Area×Cost per m2=19.6×2.25≈44.1 Rs
Heron's formula cannot be used to calculate the area of quadrilaterals.
1. (I) T
2. (II) F
3. (III) F
4. (IV) F
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - HERON'S FORMULAEXERCISE - Everyday Mathematics3videos
HERON'S FORMULA
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - COORDINATE GEOMETRY EXERCISE - ACHIEVERS SECTION (HOTS)2videos
COORDINATE GEOMETRY
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2016 SET A EXERCISE - Achievers Section5videos
IMO QUESTION PAPER 2016 SET A
Similar Questions
Find the area of a quadrilateral ABCD in which AB=3 cm, BC=4 cm, CD=4 cm, DA=5 cm and AC=5 cm.
View SolutionFind the area of a quadrilateral ABCD is which AB=3cm, BC=4cm, CD=4cm, DA=5cm and AC=5cm
S=12(a+b+c)=12(3+4+5)=6
arof ABC=sqrt(s(s-a)(s-b)(s-c)<br>ar ABC=√6(6−3)(6−4)(6−5)
⇒√6×3×2×1=6cm2
Now in △ADC,S=a+b+c2
⇒s=5+4+52=142=7cm
By using Heron’s formula
Area of △ADC=√s(s−a)(s−b)(s−c)
=√7(7−5)(7−4)(7−5)
=√7×2×3×2
=2√21cm2
Area of△ADC=9.2cm2 (approx.)
Area of the quadrilateral ABCD = Area of △ADC+Areaof△ABC=9.2cm2+6cm2=15.2cm2
Thus, the area of the quadrilateral,ABCDis15.2cm2.View SolutionFind the area of the quadrilateral ABCD in which AB=3cm,BC=4cm,CD=4cm,DA=5cm and AC=5cm.
View SolutionFind the area of the quadrilateral ABCD, in which AB=7cm, BC=6cm, CD=12 cm, DA=15cm and AC=9 cm.
View SolutionFind the area of the quadrilateral ABCD , in which AB=7cm,BC=6cm,CD=12cm,DA=15cmandAC=9cm
View SolutionConstruct a quadrilateral ABCD in which AB=3.8cm, BC=5cm,CD=5cm, DA=5.5cm and AC=8cm.
View SolutionFind the area of the quadrilateral ABCD; in which AB = 7 cm; BC =6 cm;CD =12 cm; DA= 15 cm and AC =9 cm
View SolutionFind the area of the quadrilateral ABCD in which in AB = 42 cm, BC = 21 cm, CD = 29 cm, DA = 34 cm and diagonal BD = 20 cm.
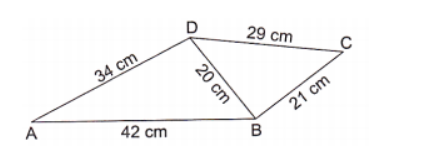 View Solution
View SolutionFind the area of quadrilateral ABCD in which ∠B=90∘, BC = 32 cm, AB = 24 cm and CD=DA = 25 cm.
View SolutionFind the area of the quadrilateral ABCD in which AB= 42 cm. Bc=21cm,CD=29cm,DA=34cmand diagonal BD= 20 cm .
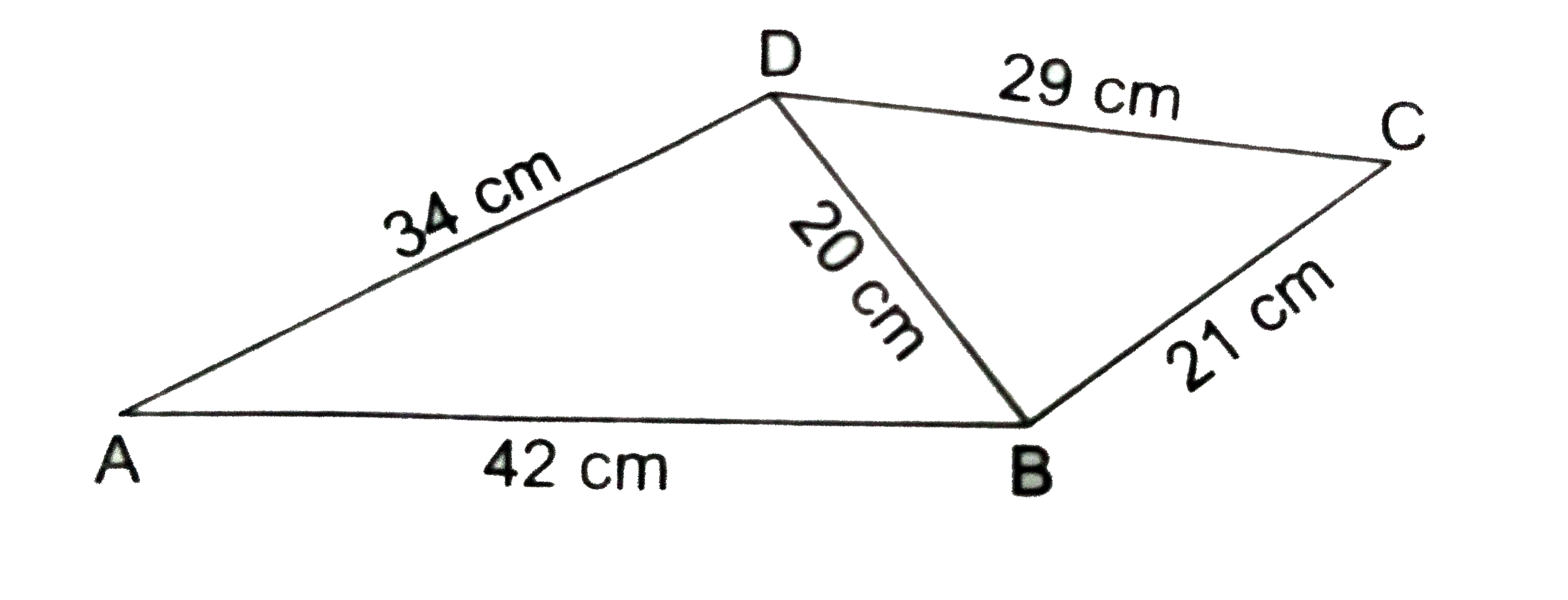 View Solution
View Solution

