A particle of mass 272 g is moved along half the circumference of a circle of radius 0.5 m. The force acting on the particle at any point has a magnitude of 10 N and is inclined at 30∘ to the tangent at that point. What is the velocity acquired by the particle ?
W=Fcosθ×πr=10×cos30∘×π×0.5=13.6J
1/2mv2=1/2×0.272×v2=13.6
v=10ms−1.
Topper's Solved these Questions
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERES
43 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS
12 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - VERY SHORT ANSWER QUESTIONS
60 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Selected problems
30 Videos
Similar Questions
A particle whose mass is 2 kg moves with a speed of 44 m/s on a curved path. The resultant force acting on the particle at a particular point of the curve is 30 N at 60∘ to the tangent to the curve, as shown in fig. At the point, find (a) the radius of curvature of the curve and (b) the tangential acceleration of the particle.
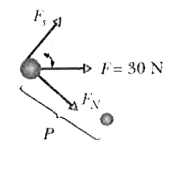
View SolutionThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance s as K=as2. The force acting on the particle is
View Solution
Knowledge Check
A particle is moving at uniform speed 2ms−1 along a circle of radius 0.5m.The centripetal acceleration of particle is
A1ms−2B2ms−2C4ms−2D8ms−2A particle moves along a semicircle of radius 10m in 5 seconds. The average velocity of the particle is
A2πms−1B4πms−1C2ms−1D4ms−1A particle is moving with a constant linear velocity 5 cm/s, on the circumference of circle of radius 10 cm. The centripetal acceleration of the particle will be
A0B2.5 cm/s2C2 cm/s2D0.5 cm/s2
A particle is moving with a constant speed v in a circle. What is the magnitude of average velocity after half rotation?
View SolutionA particle moves on the circumference of a circle of radius r. Starting from one point particle reaches to its diametric end in time t.The magnitude of average velocity of the particle is
View SolutionA particle of mass m moves along a circle of 'R'. The modulus of the average vector of force acting on the particle over the distance equal to a quarter of the circle is :
View SolutionThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance s as K=as2. The force acting on the particle is
View SolutionA particle is moving with uniform speed 0.5m/s along a circle of radius 1m then the angular velocity of particle is (in rads−1)
View Solution
