"If the slits in Young's double slit experiment are identical, then intensity at any point on the screen may vary between zero and four times to the intensity due to single slit". Justify the above statement through a relevant mathematical expression.
To justify the statement that the intensity at any point on the screen in Young's double slit experiment can vary between zero and four times the intensity due to a single slit, we can derive the relevant mathematical expression step by step.
Step 1: Understanding the Setup
In Young's double slit experiment, we have two identical slits (S1 and S2) that are illuminated by a monochromatic light source. The intensity of light from each slit is denoted as I0.
Step 2: Resultant Intensity Formula
The resultant intensity I at any point on the screen due to the two slits can be expressed using the formula for interference:
I=I1+I2+2√I1I2cosϕ
where:
- I1 is the intensity from slit S1,
- I2 is the intensity from slit S2,
- ϕ is the phase difference between the two waves arriving at the point on the screen.
Step 3: Substituting Intensities
Since both slits are identical, we have:
I1=I0andI2=I0
Substituting these values into the intensity formula gives:
I=I0+I0+2√I0I0cosϕ
This simplifies to:
I=2I0+2I0cosϕ
or
I=2I0(1+cosϕ)
Step 4: Analyzing Maximum and Minimum Intensities
The term (1+cosϕ) varies depending on the value of ϕ:
- The maximum value of cosϕ is 1, which occurs when the waves are in phase (constructive interference). Thus:
Imax=2I0(1+1)=4I0
- The minimum value of cosϕ is -1, which occurs when the waves are out of phase (destructive interference). Thus:
Imin=2I0(1−1)=0
Conclusion
From the above analysis, we can conclude that the intensity at any point on the screen can vary between:
0≤I≤4I0
This justifies the statement that the intensity at any point on the screen may vary between zero and four times the intensity due to a single slit.
In Young's double slit experiment, we have two identical slits (S1 and S2) that are illuminated by a monochromatic light source. The intensity of light from each slit is denoted as I0.
The resultant intensity I at any point on the screen due to the two slits can be expressed using the formula for interference:
I=I1+I2+2√I1I2cosϕ
where:
- I1 is the intensity from slit S1,
- I2 is the intensity from slit S2,
- ϕ is the phase difference between the two waves arriving at the point on the screen.
Since both slits are identical, we have:
I1=I0andI2=I0
Substituting these values into the intensity formula gives:
I=I0+I0+2√I0I0cosϕ
This simplifies to:
I=2I0+2I0cosϕ
or
I=2I0(1+cosϕ)
The term (1+cosϕ) varies depending on the value of ϕ:
- The maximum value of cosϕ is 1, which occurs when the waves are in phase (constructive interference). Thus:
Imax=2I0(1+1)=4I0
- The minimum value of cosϕ is -1, which occurs when the waves are out of phase (destructive interference). Thus:
Imin=2I0(1−1)=0
From the above analysis, we can conclude that the intensity at any point on the screen can vary between:
0≤I≤4I0
This justifies the statement that the intensity at any point on the screen may vary between zero and four times the intensity due to a single slit.
Topper's Solved these Questions
- BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022 TERM IIEXERCISE - SECTION B16videos
SAMPLE PAPER 2022 TERM II
- BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022EXERCISE - SECTION C6videos
SAMPLE PAPER 2022
- BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2023 TERM IEXERCISE - SECTION D4videos
SAMPLE PAPER 2023 TERM I
Similar Questions
Youngs Double slit experiment | variation of intensity on screen
View SolutionIn young's double slit experiment relative intensity at a point on the screen may be defined as ratio of intensity at that point to the maximum intensity on the screen. Light of wavelength 7500∘A A passing through a double slit, produces interference pattern of relative intensity variation as shown in Fig. θ on horizontal axis represents the angular position of a point on the screen
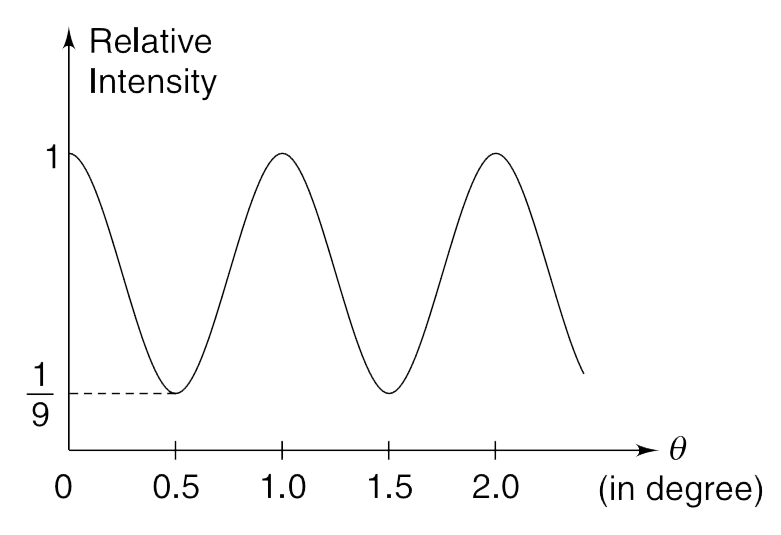
(a) Find separation d between the slits.
(b) Find the ratio of amplitudes of the two waves producing interference pattern on the screen.View Solution
Knowledge Check
- Question 1 - Select One
In a Young's double slit experiment, the central point on the screen is
ABrightBDarkCFirst bright and then darkDFirst dark and then bright - Question 2 - Select One or More
In Young's double slit experiment, phase difference between the waves at a point on screen having intensity less than the average intensity on screen may be
Aπ/4B2π/3CπD7π/8 - Question 3 - Select One
Slit widths in a young double slit experiment are in the ratio 9:4. Ratio of intensity at minima to that at maxima is
A4:9B16:81C1:25D1:16
In Young's double slit experiment, the maximum intensity is I0. What is the intensity at a point on the screen where the path difference between the interfering waves is λ4 ?
View SolutionIn the standard Young's double slit experiment, the intensity on the screen at a point distant 1.25 fringe widths from the central maximum is (assuming slits to be identical)
View SolutionIn Young's double slit experiment, if the widths of the slits are in the ratio 4:9, the ratio of the intensity at maxima to the intensity at minima will be
View SolutionIn Young's double slit experiment, if the widths of the slits are in the ratio 4:9, the ratio of the intensity at maxima to the intensity at minima will be
View SolutionIn Young's double slit experiment intensity at a point is (14) of the maximum intersity. Angular position of this point is
View Solution

