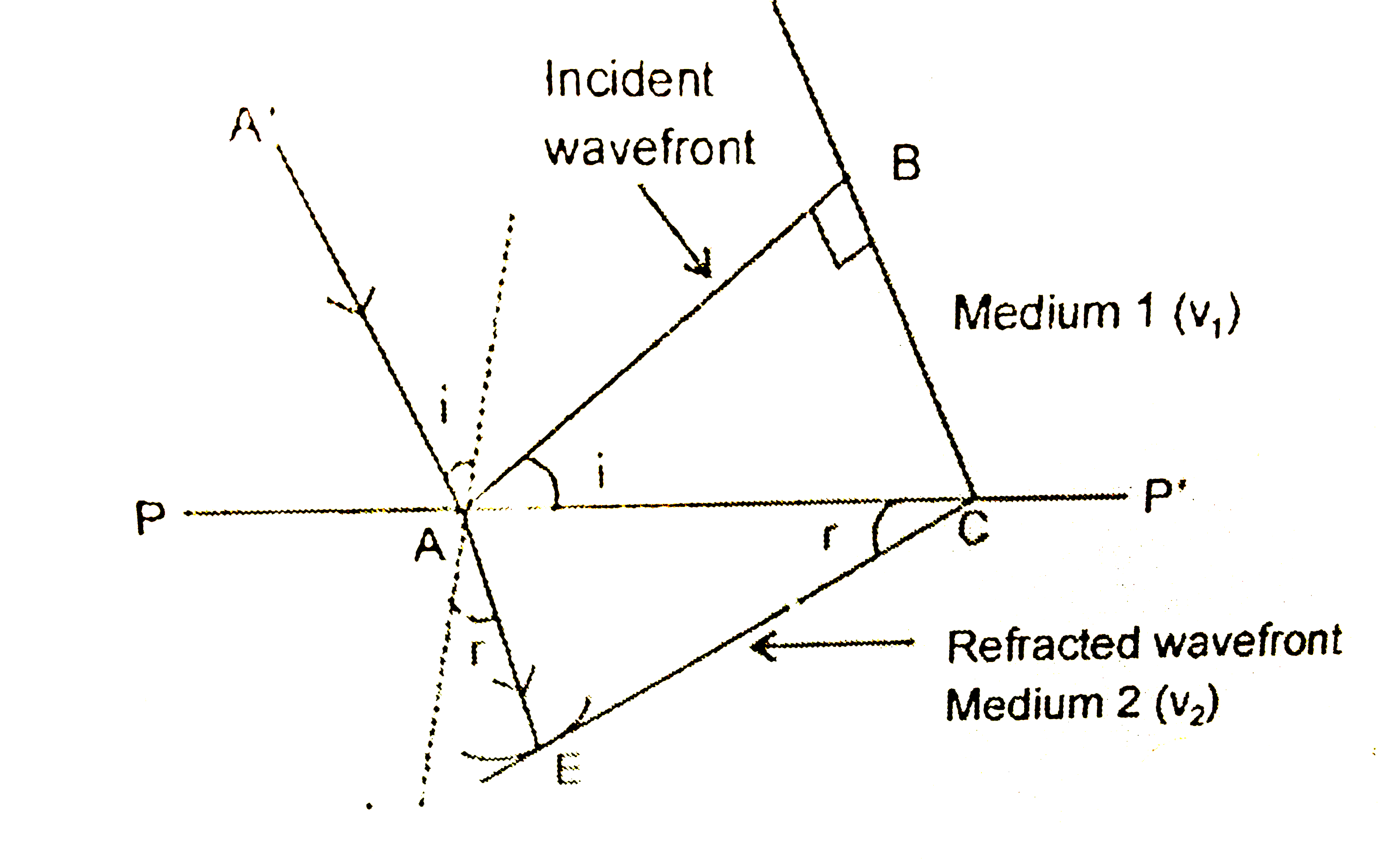
Define wavefront. Draw the shape of refracted wavefront when the plane incident wave undergoes refraction from optically denser medium to rarer medium. Hence prove Snell’s law of refraction

Video Solution

Text Solution

Generated By DoubtnutGPT

Step-by-Step Solution:
1. Definition of Wavefront:
A wavefront is defined as the locus of all points in a medium that are vibrating in the same phase of a wave. In simpler terms, it is an imaginary surface that connects all the points that are at the same stage of vibration in a wave. For example, in a plane wave, the wavefronts are parallel planes.
2. Drawing the Shape of Refracted Wavefront:
To illustrate the shape of the refracted wavefront when a plane wavefront passes from an optically denser medium to a rarer medium, we can follow these steps:
- Draw a horizontal line to represent the boundary between the two media.
- Draw a set of parallel lines above the boundary to represent the incident wavefront in the denser medium.
- When the wavefront reaches the boundary, it will bend away from the normal as it enters the rarer medium.
- Draw a new set of parallel lines in the rarer medium that are further apart than the incident wavefront lines, indicating that the wavefront has refracted.
3. Proving Snell’s Law of Refraction:
Snell's Law states that the ratio of the sine of the angle of incidence (i) to the sine of the angle of refraction (r) is constant and is equal to the ratio of the velocities of the wave in the two media:
$\frac{sin i}{sin r} = \frac{v_{1}}{v_{2}} = \frac{n_{2}}{n_{1}}$
where $n_{1}$ and $n_{2}$ are the refractive indices of the two media.
- Let’s consider two points A and B on the wavefront in the denser medium and their corresponding points A' and B' in the rarer medium after refraction.
- The time taken for the wave to travel from A to A' and from B to B' is the same.
- The distances traveled in the two media can be expressed as:
- In the denser medium: $d_{1} = v_{1} \cdot t$
- In the rarer medium: $d_{2} = v_{2} \cdot t$
- The relationship between the angles and the distances can be derived using trigonometric relations from the geometry of the situation:
$\frac{d_{1}}{d_{2}} = \frac{v_{1} \cdot t}{v_{2} \cdot t} = \frac{v_{1}}{v_{2}}$
- Using the definitions of sine in the context of the angles of incidence and refraction, we can relate the distances to the angles:
$\frac{d_{1}}{d_{2}} = \frac{sin i}{sin r}$
- Equating both expressions gives us Snell's Law:
$\frac{sin i}{sin r} = \frac{v_{1}}{v_{2}}$

Updated on:8/8/2024