A diver in water looks obliquely at an object AB in air.
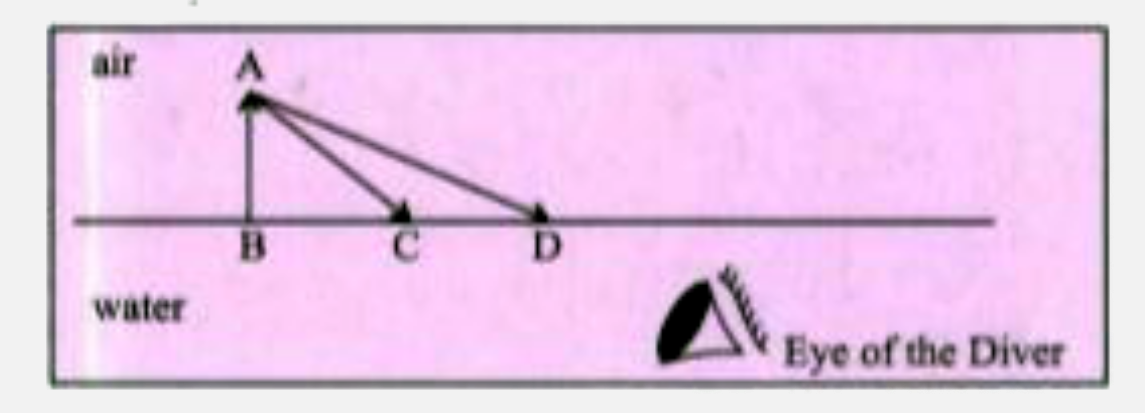
Show the path of two rays AC and AD starting from the tip of the object as it travels towards the diver in water and hence obtain the image of the object.
Step by step video & image solution for A diver in water looks obliquely at an object AB in air. Show the path of two rays AC and AD starting from the tip of the object as it travels towards the diver in water and hence obtain the image of the object. by Physics experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A diver in water looks obliquely at an object AB in air.
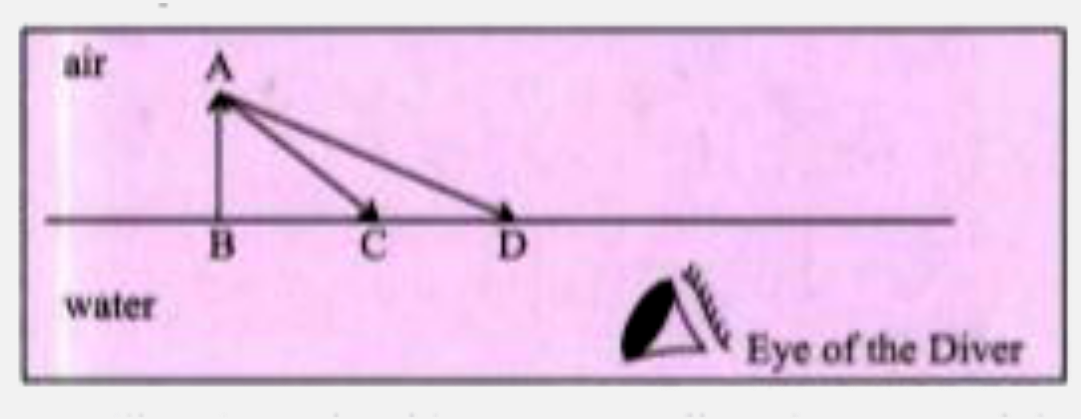
Does the object appear taller, shorter or of the same size to the diver?
View Solution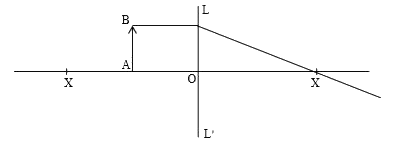
Copy and complete the ray diagram to show the formation of the image of the object AB
View SolutionA : When a diver under water looks obliquely at a fisherman standing on the bank of a lake then fisherman looks taller.
R : When a ray of light travelling in air enters water, it bends towards the normal.
View SolutionTo construct a ray diagram we use two rays of light which are so chosen that it is easy to determine their directions after reflection from the mirror. Choose these two ras and state the path of these rays after reflection from a concave mirror . Use these two rays to find the nature and position of the image of an object plced at a distance of 15 cm from a concave mirror of focal length 10 cm.
View SolutionIn figure, PQ and PR are the two light rays emerging from an object P. the ray PQ is refracted as QS.
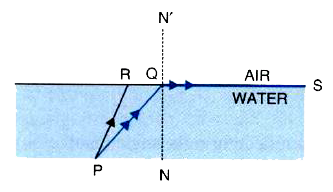
(a) state the special name given to the angle of incidence ∠PQN for the ray PQ.
(b) What is the angle of refraction for the refracted ray QS?
(c) Name the phenomenono that occurs if the angle of incidence ∠PQN is increased.
(d) The ray PR suffers partial reflection and refraction on the water-air surface. give reason.
(e) Draw in the diagram the refracted ray for the incident ray PR and hence show the position of the image of the object P by the letter P' when seen vertically from above.
View SolutionA thin lens, made of glass of refractive index 3/2, produces a real and magnified image of an object in air. If the whole system, maintaing the same distance between the object and the lens, is immersed in water (RI=4/3), then the image formed will be
View SolutionTwo towers AB and CD are situated a distance d apart as shown in figure. AB is 20 m high and CD is 30 m high from the ground. An object of mass m is thrown from the top of AB horizontally with a velocity of 10 m/s towards CD. Simultaneously another object of mass 2 m is thrown from the top of CD at an angle 60∘ below the horizontal towards AB with the same magnitude of initial velocity as that of the first object. The two objects move in the same vertical plane, collide in mid-air and stick to each other.

Find the distance from B where the objects hit the ground.
View SolutionTwo towers AB and CD are situated a distance d apart as shown in figure. AB is 20 m high and CD is 30 m high from the ground. An object of mass m is thrown from the top of AB horizontally with a velocity of 10 m/s towards CD. Simultaneously another object of mass 2 m is thrown from the top of CD at an angle 60∘ below the horizontal towards AB with the same magnitude of initial velocity as that of the first object. The two objects move in the same vertical plane, collide in mid-air and stick to each other.

Calculate the distance d between the towers.
View SolutionOne end of a cylindrical glass rod (mu = 1.5) of radius 1.0 cm is rounded in the shape of a hemisphere. The rod is immersed in water (mu= 4/3) and an object is placed in the water along the axis of the rod at a distance of 8.0 cm from the rounded edge. Locate the image of the object.
View SolutionTo construct a ray diagram, we use two rays which are so chosen that it is easy to know their directions after reflection from the mirror. List two such rays and state the path of these rays after reflection in case of concave mirrors. Use these two rays and draw ray diagram to locate the image of an object placed between pole and focus of a concave mirror.
View Solution
