Two towers AB and CD are situated a distance d apart as shown in figure. AB is 20 m high and CD is 30 m high from the ground. An object of mass m is thrown from the top of AB horizontally with a velocity of 10 m/s towards CD. Simultaneously another object of mass 2 m is thrown from the top of CD at an angle 60∘ below the horizontal towards AB with the same magnitude of initial velocity as that of the first object. The two objects move in the same vertical plane, collide in mid-air and stick to each other.

Find the distance from B where the objects hit the ground.
The correct Answer is:20√3m
Applying conservation of linear momentum (during collision of the masses at M) in the horizontal direction
m×10−2m×5=3m×Vx ⇒10m−10m=3m×Vx⇒0
Since the horizontal momentum comes out to be zero, the combination of masses will drop vertically downwards and fall at E.
BE=PM=10t=10×2√3=11.54m
Method 2 :
Acceleration of A and C both is 10m/s2 downwards.
Therefore, relative acceleration between them is zero, i.e., the relative motion between them will be a straight line.
Now assuming A to be at rest, the condition of collision will be that →vCA=→vC−→vA = relative velocity of C w.r.t A should be along CA.
→vA=10ˆi
→vC=−5ˆi−5√3ˆj
→vCA=−5ˆi−5√3ˆj−10ˆi ∴→vCA=−15ˆi−5√3ˆj
⇒tanθ=155√3=√3⇒θ=60∘
∴tan60∘=d10 ∴d=10√3m

Topper's Solved these Questions
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - PARAGRAPH QUESTIONS
5 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - ASSERTION & REASON TYPE
1 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE MAIN (ARCHIVE)
53 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
111 Videos
Similar Questions
Two towers AB and CD are situated a distance d apart as shown in figure. AB is 20 m high and CD is 30 m high from the ground. An object of mass m is thrown from the top of AB horizontally with a velocity of 10 m/s towards CD. Simultaneously another object of mass 2 m is thrown from the top of CD at an angle 60∘ below the horizontal towards AB with the same magnitude of initial velocity as that of the first object. The two objects move in the same vertical plane, collide in mid-air and stick to each other.

Calculate the distance d between the towers.
View SolutionA ball is thrown upwards from the top of a tower 40m high with a velocity of 10m/s. Find the time when it strikes the ground. Take g=10m/s2.
View SolutionA ball is thrown upwards from the top of a tower 40m high with a velocity of 10m/s. Find the time when it strikes the ground. Take g=10m/s2.
View SolutionA stone is thrown from the top of a tower at an angle of 30∘ above the horizontal level with a velocity of 40 m/s. it strikes the ground after 5 second from the time of projection then the height of the tower is
View SolutionA ball of mass m is thrown at an angle of 45∘ to the horizontal,, from the top of a 65m high tower AB as shown in Fig. at t=0. Another identical ball is thrown with velocity 20m/s horizontally towards AB from the top of a 30m high tower CD1s after the projection of the first ball. Both the balls move the same vertical plane. If they collide in mid-air,

the distance AC is
View SolutionA ball of mass m is thrown at an angle of 45∘ to the horizontal,, from the top of a 65m high tower AB as shown in Fig. at t=0. Another identical ball is thrown with velocity 20m/s horizontally towards AB from the top of a 30m high tower CD1s after the projection of the first ball. Both the balls move the same vertical plane. If they collide in mid-air,

the two balls will collide at time t=
View SolutionA ball of mass 2kg is thrown with velocity 10ms at an angle of 30°to the horizontal and another ball with the same mass is thrown at an angel of 60° to the horizontal with the same speed.The ratio will be their range will be
View SolutionA ball of mass m is thrown at an angle of 45∘ to the horizontal,, from the top of a 65m high tower AB as shown in Fig. at t=0. Another identical ball is thrown with velocity 20m/s horizontally towards AB from the top of a 30m high tower CD1s after the projection of the first ball. Both the balls move the same vertical plane. If they collide in mid-air,

the height from the ground where the two balls will collide is
View SolutionA ball of mass m is thrown at an angle of 45∘ to the horizontal,, from the top of a 65m high tower AB as shown in Fig. at t=0. Another identical ball is thrown with velocity 20m/s horizontally towards AB from the top of a 30m high tower CD1s after the projection of the first ball. Both the balls move the same vertical plane. If they collide in mid-air,

. the velocity of combined ball just after they struck together is
View SolutionA ball is thrown from the top of 36m high tower with velocity 5m/ss at an angle 37∘ above the horizontal as shown. Its horizontal distance on the ground is closest to [g=10m/s2
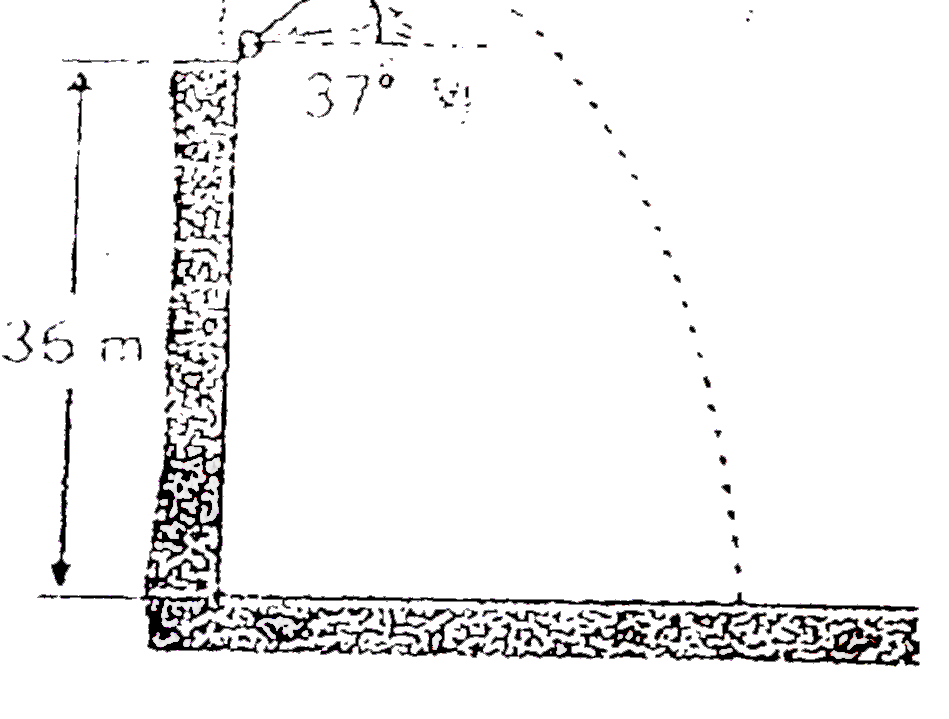 :
:
View Solution
