△ABC is an isosceles triangle with side AB=AC. P,Q and R are the midpoints of AB,BC and CA, respectively. What is the congruence condition that proves △RBC≅△PCB ?
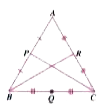
The correct Answer is:△PBC≅△RCB
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLESBOOK - ICSECHAPTER - CONGRUENCE OF TRIANGLESEXERCISE - EXERCISE 13.1
7 Videos
- CONGRUENCE OF TRIANGLESBOOK - ICSECHAPTER - CONGRUENCE OF TRIANGLESEXERCISE - EXERCISE 13.2
11 Videos
- CONGRUENCEBOOK - ICSECHAPTER - CONGRUENCEEXERCISE - EXERCISE 21
23 Videos
- CONSTRUCTION BOOK - ICSECHAPTER - CONSTRUCTION EXERCISE - EXERCISE
18 Videos
Similar Questions
Knowledge Check
In the adjoining figure, ABC is an isosceles triangle in which AB=AC. If E and F be the midpoints of AC and AB respectively, then
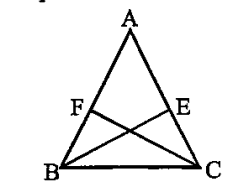 ABE=CFB∠BFC=∠CEBCBF=CEDAll of these
ABE=CFB∠BFC=∠CEBCBF=CEDAll of theseIn the adjoining figure, ABC is an isosceles triangle in which AB = AC. If E and F be the midpoints of AC and AB respectively, then
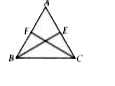 ABE = CFB∠BFC=∠CEBCBF = CEDAll of these
ABE = CFB∠BFC=∠CEBCBF = CEDAll of theseIf △ABC is an isosceles triangle with ∠c=90∘ and AC = 5 cm then AB is:
A5 cmB2.5 cmC10 cmD5√2cm
In the given triangle P, Q and R are the mid points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.

View SolutionABC is an isosceles triangle with AB=AC and D is a point on AC such that BC2=ACxCD. Prove that BD=BC
View SolutionThe incircle of an isoceles triangle ABC, with AB=AC, touches the sides AB,BC and CA at D,E and F respecrively. Prove that E bisects BC.
View SolutionΔABC is an equilateral triangle, AB = 6. The points P, Q and Rare midpoints of AB, BC and CA respectively. The perimeter of PBCR is
View SolutionABC is an equilateral triangle. P,Q and R are the midpoints of sides AB, BC and CA respectively. If the length of the side of the triangle ABC is 8 cm, then the area of △PQR is:
ABC एक समबाहु त्रिभुज है | P, Q और R क्रमशः भुजाओं AB, BC तथा CA के मध्य बिंदु हैं | यदि त्रिभुज ABC की भुजा की लंबाई 8 सेमी है, तो त्रिभुज PQR का क्षेत्रफल कितना होगा ?
View Solution
