The incircle of an isoceles triangle ABC, with AB=AC, touches the sides AB,BC and CA at D,E and F respecrively. Prove that E bisects BC.
Step by step video & image solution for The incircle of an isoceles triangle ABC, with AB=AC, touches the sides AB,BC and CA at D,E and F respecrively. Prove that E bisects BC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Revision Exercise Very Short Answer Question
7 Videos
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Revision Exercise Short Answer Questions
4 Videos
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Problems From NCERT/exemplar
11 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions
10 Videos
Similar Questions
In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F respectively. If AB= 12 cm, BC= 8 cm and AC = 10 cm, find the lengths of AD, BE and CF.
View SolutionLet the incircle of a ΔABC touches sides BC, CA and AB at D,E and F, respectively. Let area of ΔABC be Δ and thatof DEF be Δ'. If a, b and c are side of DetlaABC, then the value of abc(a+b+c)Δ'Δ3 is
View SolutionThe sides AB and AC are equal of an isosceles triangle ABC. D E and F are the mid-points of sides BC, CA and AB respectively. Prove that:
(i) Line segment AD is perpedicular to line segment EF.
(ii) Line segment AD bisects the line segment EF.
View SolutionIncircle of ΔABC touches the sides BC, AC and AB at D, E and F, respectively. Then answer the following question
∠DEF is equal to
View SolutionIncircle of ΔABC touches the sides BC, AC and AB at D, E and F, respectively. Then answer the following question
The length of side EF is
View SolutionABC is a triangle A line is drawn parallel to BC to meet AB and AC in D and E respectively. Prove that the median through A bisects DE.
View SolutionLet s denotes the semi-perimeter of a ΔABC in which BC=a, CA=b and AB=c. If a circle touches the sides BC, CA, AB, at D, E, F, respectively. Prove that BD=s-b.
View SolutionA circle is touching the side BC of a △ABC at point P and touching AB and AC produced at Q and R respectively. Prove that AQ=12(perimeter of △ABC).
View SolutionIncircle of ABC touches the sides BC, CA and AB at D, E and F, respectively. Let r1 be the radius of incircle of BDF. Then prove that r1=12(s−b)sinB(1+sin(B2))
View SolutionIn figureE is a point on side CB produced of an isosceles △ABC with AB=AC. If AD⊥BCandEF⊥AC, prove thatΔABD~ΔECF.
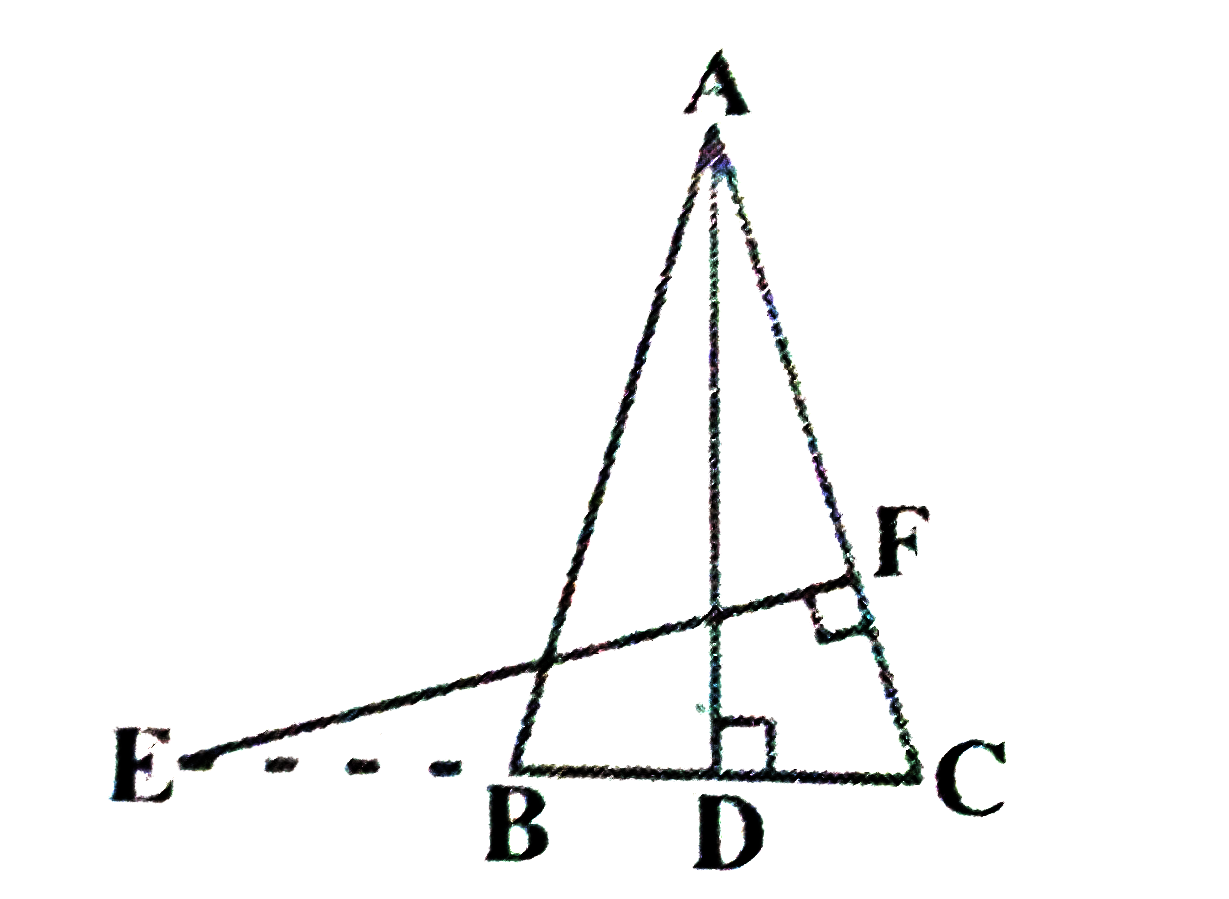
View Solution
