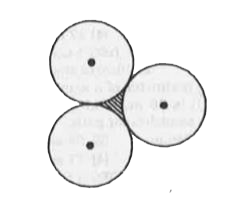
There are three equal circles of unit radii touching each other.
Find the area of the triangle circumscribing the three circles.
√3(√3+1)2
(√3+1)2
√3(√3+1)
None of these
The correct Answer is:A
Topper's Solved these Questions
- GEOMETRY BOOK - DISHA PUBLICATIONCHAPTER - GEOMETRY EXERCISE - TEST YOURSELF
3 Videos
- GEOMETRY BOOK - DISHA PUBLICATIONCHAPTER - GEOMETRY EXERCISE - Practice Exercises (Standard Level)
21 Videos
- FundamentalsBOOK - DISHA PUBLICATIONCHAPTER - FundamentalsEXERCISE - Test Yourself
15 Videos
- INEQUALITIESBOOK - DISHA PUBLICATIONCHAPTER - INEQUALITIESEXERCISE - Test Yourself
15 Videos
Similar Questions
Knowledge Check
Three equal circles of unit radius touch each other. Then, the area of the circle circumscribing the three circles is:
A6π(2+√3)2Bπ6(2+√3)2Cπ3(2+√3)2D3π(2+√3)2Three equal circles of unit radius touch each other. Then, the area of the circle circumscribing the three circles is:
A6π(2+√3)2Bπ6(2+√3)2Cπ3(2+√3)2D3π(2+√3)2Three equal circles of unit radius touch each other. Then, the area of the circles is
Aπ3(2+√3)3B2π3(2+√3PP2)C6π(2+√3)2D16π(2+√3)2
Three equal circles of radius unity touches one another. Radius of the circle touching all the three circles is:
View SolutionABC is a triangle with AB=10cm, BC=8cm and AC=6cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres Find the radii of the three circles.
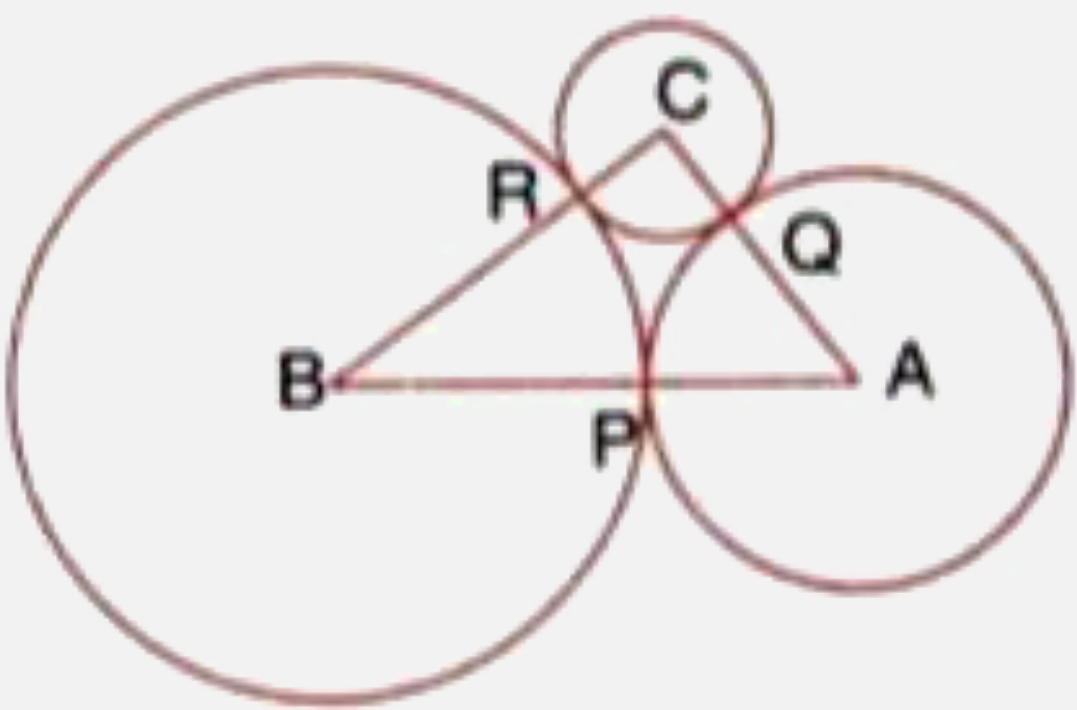
View SolutionThe circles having radii 1,2,3, touch each other externally then find the radius of the circle which cuts the three circles orthogonally
View SolutionThree circles of radius a, b, c touch each other externally. The area of the triangle formed by joining their centre is
View SolutionIf the four equal circles of radius 3 cm touch each other externally, then the area of the region bounded by the four circles is
View Solution