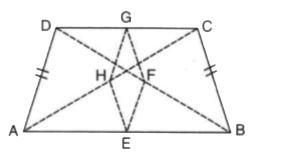
In any quadrilateral ABCD, the diagonal AC and BD intersect at a point X. If E, F, G and H are the mid-points of AX, BX, CX and DX respectively, then what is the ratio of (EF + FG + GH + GE) to (AD + DC + CB + BA)?
12
32
34
Date insufficient
The correct Answer is:A
Topper's Solved these Questions
- GEOMETRY BOOK - DISHA PUBLICATIONCHAPTER - GEOMETRY EXERCISE - TEST YOURSELF
3 Videos
- GEOMETRY BOOK - DISHA PUBLICATIONCHAPTER - GEOMETRY EXERCISE - Practice Exercises (Standard Level)
21 Videos
- FundamentalsBOOK - DISHA PUBLICATIONCHAPTER - FundamentalsEXERCISE - Test Yourself
15 Videos
- INEQUALITIESBOOK - DISHA PUBLICATIONCHAPTER - INEQUALITIESEXERCISE - Test Yourself
15 Videos
Similar Questions
Knowledge Check
ABCD is a parallelogram. The diagonals AC and BD intersect at a point O. If E,F,GandH are the mid-points of AO,DO,COandBO respectively, then the ratio of (EF+FG+GH+HE) to (AD+DC+CB+BA) is:
A1:1B1:2C1:3D1:4ABCD is a parallelogram in which diagonals AC and BD intereset at O. If E, F, G and H are the mid points of AO, DO, CO and BO respectively, then the ratio of the perimeter of the quadrilateral EFGH to the perimeter of parallelogram ABCD is:
A0.042361111111111B0.043055555555556C0.04375D0.044444444444444ABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :
 A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2
A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2
In quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE:EC=BE:ED.
Show that : ABCD is a trapezium.
View Solution□ABCD is a parallelogram. The diagonals AC and BD intersect at point M. The length of seg AC, AB and AD is 24, 22 and 34 respectively. Find the length of seg BD.
View SolutionD is any point on side AC of ΔABC. If P,Q, X, Y are the mid points of AB,BC,ADandDCrespectively, then the ratio of PXandQYis
View SolutionABCD is a parallelogram in which diagonals AC and BD intereset at O. If E, F, G and H are the mid points of AO, DO, CO and BO respectively, then the ratio of the perimeter of the quadrilateral EFGH to the perimeter of parallelogram ABCD is:
View Solution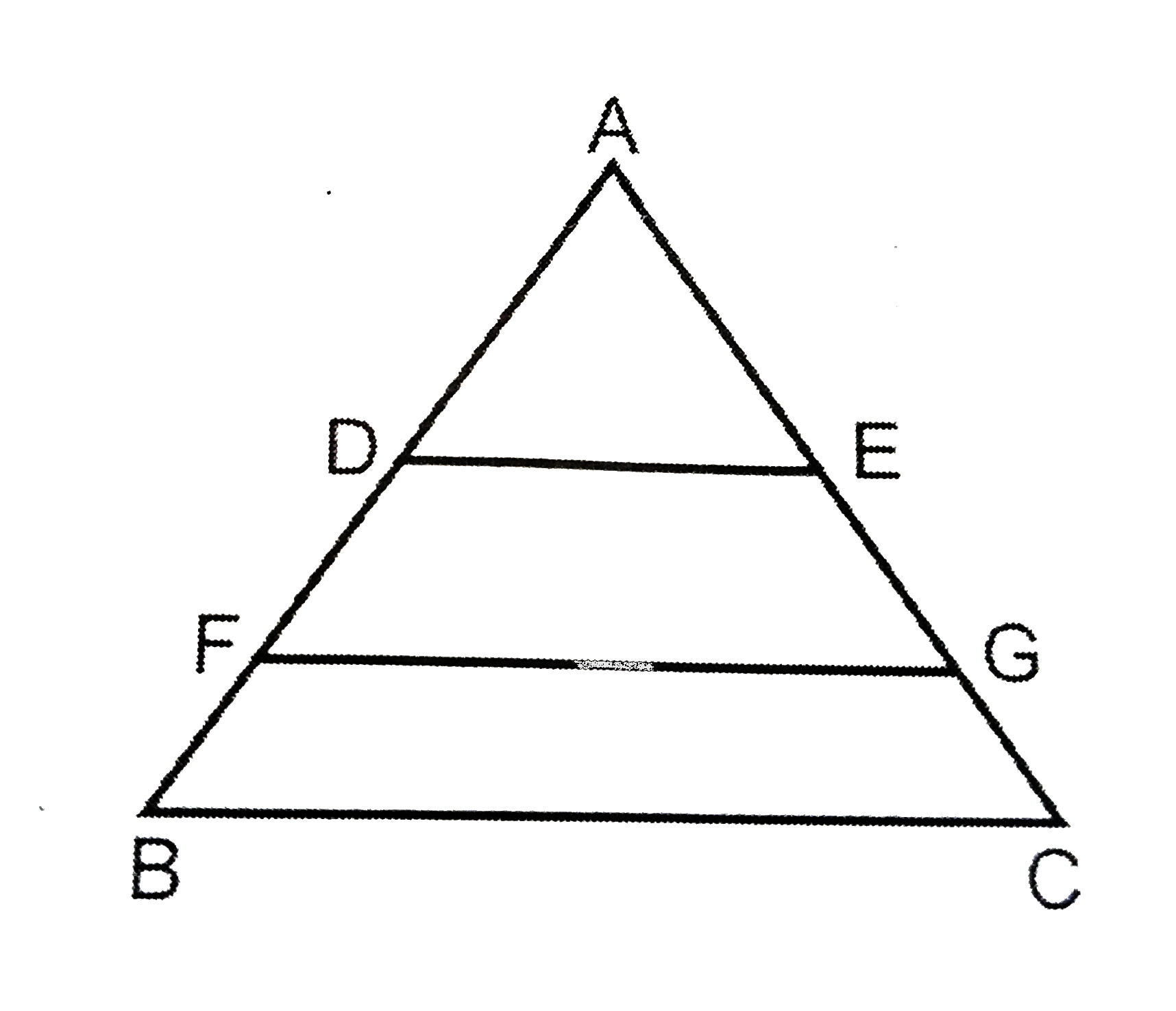
In ΔABC,D and E are the mid-points of AB and AC. Again, F and G are the mid-points of DB and EC, If BC=12,what is the length of FG?
View Solution