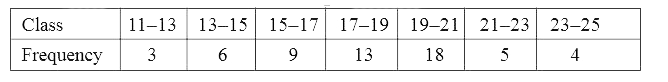The mean and median of a distribution are both equal to 635.97 . Find the mode.
Text Solution
The correct Answer is:635.97
|
Topper's Solved these Questions
- STATISTICS AND PROBABILITYBOOK - EDUCART PUBLICATIONCHAPTER - STATISTICS AND PROBABILITYEXERCISE - SHORT ANSWERS (SA-I) Type Questions
45 Videos
- STATISTICS AND PROBABILITYBOOK - EDUCART PUBLICATIONCHAPTER - STATISTICS AND PROBABILITYEXERCISE - SHORT ANSWERS (SA-II) Type Questions
58 Videos
- STATISTICS AND PROBABILITYBOOK - EDUCART PUBLICATIONCHAPTER - STATISTICS AND PROBABILITYEXERCISE - OBJECTIVE QUESTIONS (FILL IN THE BLANKS)
10 Videos
- SAMPLE QUESTION PAPER 02BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE QUESTION PAPER 02EXERCISE - SECTION - D
9 Videos
- SURFACE AREAS AND VOLUMESBOOK - EDUCART PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS
30 Videos
Similar Questions
Knowledge Check
Mean and median of a simple distribution are 38 and 39 respectively. Then, mode will be
A36B37C41D40The mean and mode of a frequency distribution are 28 and 16 respectively .The median is
A22B23.5C24D24.5The mean and median of a moderately skewed distribution are 5 and 6 respectively. Then the value of mode in such a situation is approximately equal to
A8B11C16DNone of these
In an asymmetrical distribution mean is 58 and median is 61. Find mode.
View SolutionIf the mean and mode of a frequency distribution be 53.4 and 55.2 respectively, find the median
View SolutionThe median and mode of a frequency distribution are 26 and 29 respectively. Then , the mean is
View SolutionIn the following question, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): If the median and mode of a frequency distribution are 150 and 154 respectively. Then its mean is 148.
Reason (R): Mean, median and mode of a frequency distribution are related as 3Mean=3Median - Mode.
View SolutionThe mode of a distribution is 24 and the mean is 60. Whatis its median?
View Solution