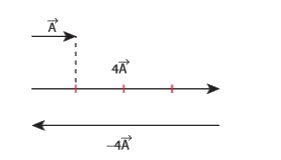
A vector →A is is given as in the following Figure. Find 4→A and −4→A
In physics, certain vector quantities can be defi ned as a scalar times another vector quantity.
Topper's Solved these Questions
- KINEMATICSBOOK - NCERT TAMILCHAPTER - KINEMATICSEXERCISE - EXERCISE (I. Multi Choice Question)
15 Videos
- KINEMATICSBOOK - NCERT TAMILCHAPTER - KINEMATICSEXERCISE - EXERCISE (IV. Exercises )
20 Videos
- HEAT AND THERMODYNAMICSBOOK - NCERT TAMILCHAPTER - HEAT AND THERMODYNAMICSEXERCISE - EVALUATION (Numerical Problems)
13 Videos
- KINETIC THEORYBOOK - NCERT TAMILCHAPTER - KINETIC THEORYEXERCISE - ADDITIONAL EXERCISE
4 Videos
Similar Questions
If →a,→band→c are three non-zero, non-coplanar vectors,then find the linear relation between the following four vectors : →a−2→b+3→c,2→a−3→b+4→c,3→a−4→b+5→c,7→a−11→b+15→c.
View SolutionIf →a,→band→c are three non-zero, non-coplanar vectors,then find the linear relation between the following four vectors : →a−2→b+3→c,2→a−3→b+4→c,3→a−4→b+5→c,7→a−11→b+15→c.
View Solution
Knowledge Check
If ∣∣→A∣∣=4,∣∣→B∣∣=3andθ=60∘ in the figure . Find
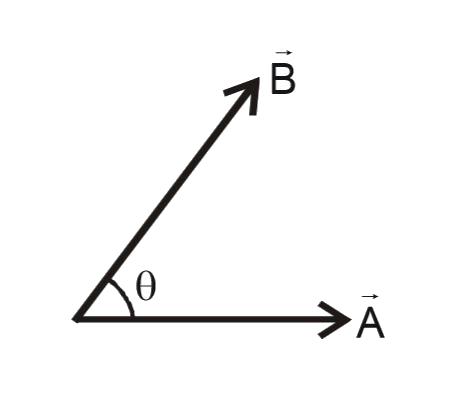
→A.→BA6B3C9D12Vectors →Aand→B satisfying the vector equation →A+→B=→a,→A×→B=→band→A.→a=1. Vectors and →b are given vectosrs, are
A→A=(→a×→b)−→aa2B→B=(→b×→a)+→a(a2−1)a2C→A=(→a×→b)+→aa2D→B=(→b×→a)−→a(a2−1)a2Vectors →Aand→B satisfying the vector equation →A+→B=→a,→A×→B=→band→A.→a=1. Vectors and →b are given vectosrs, are
A→A=(→a×→b)−→aa2B→B=(→b×→a)+→a(a2−1)a2C→A=(→a×→b)+→aa2D→B=(→b×→a)−→a(a2−1)a2
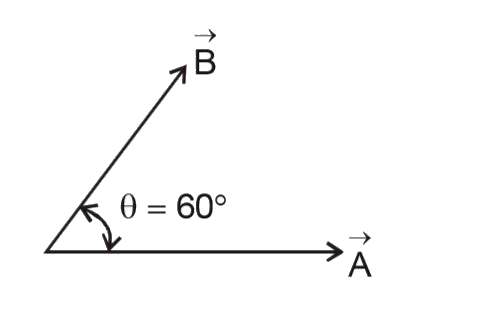
Find →A+→Band→A−→B in the diagram shown in figure. Given A = 4 units and B = 3 units.
View SolutionVectors →Aand→B satisfying the vector equation →A+→B=→a,→A×→B=→band→A.→a=1. where veca and →b are given vectosrs, are
View SolutionIf →a,→b,→c are non zero and non coplanar vectors show that the following vector are coplanar: 4→a+5→b+→c,−→b−→c,5→a+9→b+4→c
View SolutionIf →a,→b,→c are non zero and non coplanar vectors show that the following vector are coplanar: 4→a+5→b+→c,−→b−→c,5→a+9→b+4→c
View SolutionConsider three vectors →a,→band→c. Vectors →aand→b are unit vectors having an angle θ between them For vector →a,|→a|2=→a.→a If →a⊥→band→a⊥→cthen→a∣∣→b×→c If →a∣∣→b,then→a=t→b Now answer the following question: If |→c|=4,θ=cos−1(14)and→c=2→b+t→a,thent= (A) 3,−4 (B) −3,4 (C) 3,4 (D) −3,−4
View Solution
