A spring is compressed between two toy carts of masses m1 and m2. When the toy carts are released then spring exerts equal and opposite average force on each for the same time t. Assume that there is no friction between the toy carts and the ground, the velocities of toy carts are
In opposite directions but in inverse ratio of their masses
In opposite directions but in direct ratio of their masses
Equal and in opposite direction
Equal and in same direction.
The correct Answer is:A
To solve the problem of the velocities of the toy carts after the spring is released, we can follow these steps:
Step 1: Understand the System
Initially, both toy carts of masses m1 and m2 are at rest with a compressed spring between them. When the spring is released, it exerts equal and opposite forces on both carts.
Step 2: Apply Newton's Third Law
According to Newton's Third Law, the force exerted by the spring on cart 1 is equal in magnitude and opposite in direction to the force exerted on cart 2. Therefore, if the force exerted by the spring is F, we have:
F=kx
where k is the spring constant and x is the compression of the spring.
Step 3: Calculate the Acceleration of Each Cart
Using Newton's second law, we can find the acceleration of each cart:
- For cart 1:
a1=Fm1=kxm1
- For cart 2:
a2=Fm2=kxm2
Step 4: Use the Kinematic Equation
Since both carts start from rest, we can use the kinematic equation to find their velocities after time t:
- For cart 1:
v1=u+a1t=0+(kxm1)t=kxtm1
- For cart 2:
v2=u+a2t=0+(kxm2)t=kxtm2
Step 5: Determine the Direction of Velocities
Since the spring pushes the carts in opposite directions, we can assign directions:
- Let v1 be in the positive direction.
- Let v2 be in the negative direction.
Thus, we can write:
v1=kxtm1
v2=−kxtm2
Step 6: Find the Ratio of Velocities
To find the ratio of the velocities:
v1v2=kxtm1−kxtm2=−m2m1
This shows that the velocities are inversely proportional to their masses.
Conclusion
The velocities of the toy carts after the spring is released are:
- v1=kxtm1 (in one direction)
- v2=−kxtm2 (in the opposite direction)
Initially, both toy carts of masses m1 and m2 are at rest with a compressed spring between them. When the spring is released, it exerts equal and opposite forces on both carts.
According to Newton's Third Law, the force exerted by the spring on cart 1 is equal in magnitude and opposite in direction to the force exerted on cart 2. Therefore, if the force exerted by the spring is F, we have:
F=kx
where k is the spring constant and x is the compression of the spring.
Using Newton's second law, we can find the acceleration of each cart:
- For cart 1:
a1=Fm1=kxm1
- For cart 2:
a2=Fm2=kxm2
Since both carts start from rest, we can use the kinematic equation to find their velocities after time t:
- For cart 1:
v1=u+a1t=0+(kxm1)t=kxtm1
- For cart 2:
v2=u+a2t=0+(kxm2)t=kxtm2
Since the spring pushes the carts in opposite directions, we can assign directions:
- Let v1 be in the positive direction.
- Let v2 be in the negative direction.
v1=kxtm1
v2=−kxtm2
To find the ratio of the velocities:
v1v2=kxtm1−kxtm2=−m2m1
This shows that the velocities are inversely proportional to their masses.
The velocities of the toy carts after the spring is released are:
- v1=kxtm1 (in one direction)
- v2=−kxtm2 (in the opposite direction)
Topper's Solved these Questions
- NSO QUESTION PAPER 2017 SET A BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - NSO QUESTION PAPER 2017 SET A EXERCISE - ACHIEVERS SECTION
1 Videos
- NSO QUESTION PAPER 2016 SET BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - NSO QUESTION PAPER 2016 SET BEXERCISE - ACHIEVERS SECTION
2 Videos
- NSO QUESTION PAPER 2017 SET B BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - NSO QUESTION PAPER 2017 SET B EXERCISE - ARCHIEVERS SECTION
2 Videos
Similar Questions
A spring is compressed between two toy carts of mass m1 and m2. When the toy carts are released, the springs exert equal and opposite average forces for the same time on each toy cart. If v1 and v2 are the velocities of the toy carts and there is no friction between the toy carts and the ground, then :
View SolutionA spring is compressed by a toy cart of mass 150g. On releasing the cart, it moves with a speed of 0.2m/s. Calculate the elastic potential energy of the spring.
View Solution
Knowledge Check
A spring is compressed between two toy carts to masses m1 and m2. When the toy carts are released, the spring exerts on each toy cart equal and opposite forces for the same small time t. If the coefficients of friction μ between the ground and the toy carts are equal, then the magnitude of displacements of the toy carts are in the ratio
A(a) S1S2=m2m1B(b) S1S2=m1m2C(c) S1S2=(m2m1)2D(d) S1S2=(m1m2)2A spring connects two particles of masses m1 and m2 A horizontal force F acts on m1 Ignoring friction when the elongation of the spring is x then [when the spring has maximum elongation]
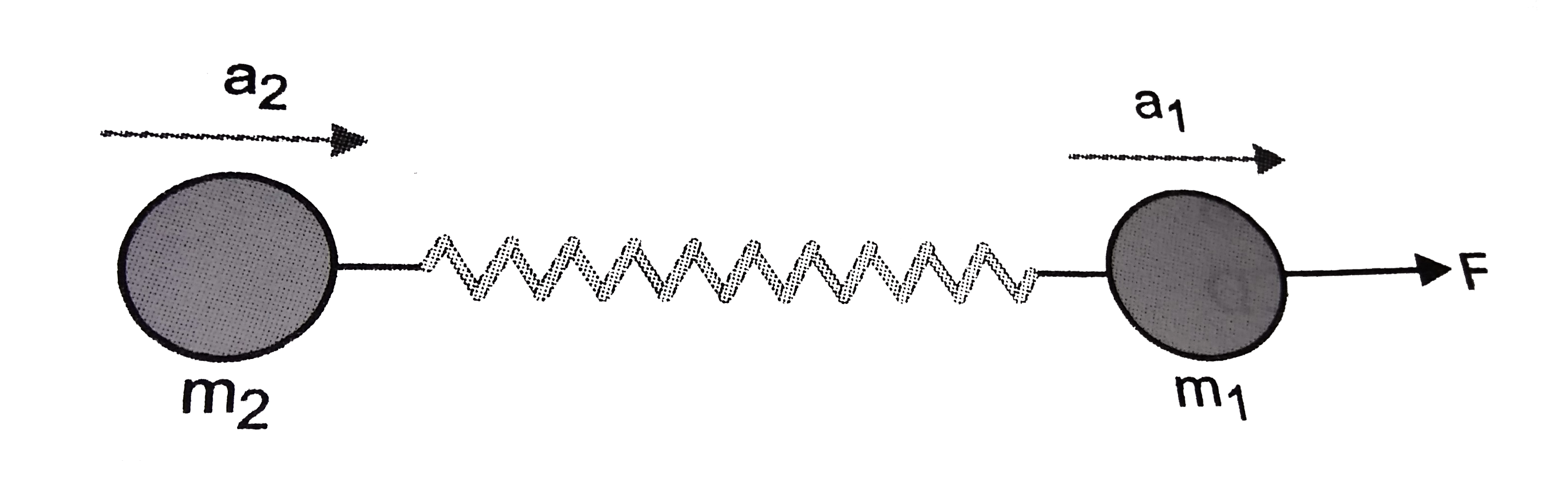 .Aa2=Kx/m2Ba1=(F−Kx)/m1CF=m1a1+m2a2Da1=a2=F(m1+m2)
.Aa2=Kx/m2Ba1=(F−Kx)/m1CF=m1a1+m2a2Da1=a2=F(m1+m2)A boy of mass 50 kg jumps with horizontal velocity of 1 m/s on to a stationary cart. If mass of the cart will be [Assume friction between the wheels the cart and road is zero ]
A1011 m/sB1110 m/sC0⋅65 m/sD0⋅8 m/s
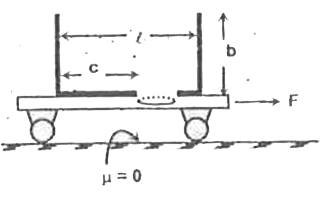
A vessel with a hole in its bottom is fastened on a cart. The mass of the vessel and the cart is M and the area of the vessel base is A . What force F should the cart be puuled with so that maximum amount of water remains in the vessel ? The dimensions of the vessel are shown in the figure . Assume where is no friction between cart and ground and vessel is fixed with cart . ( ρ is density of water )
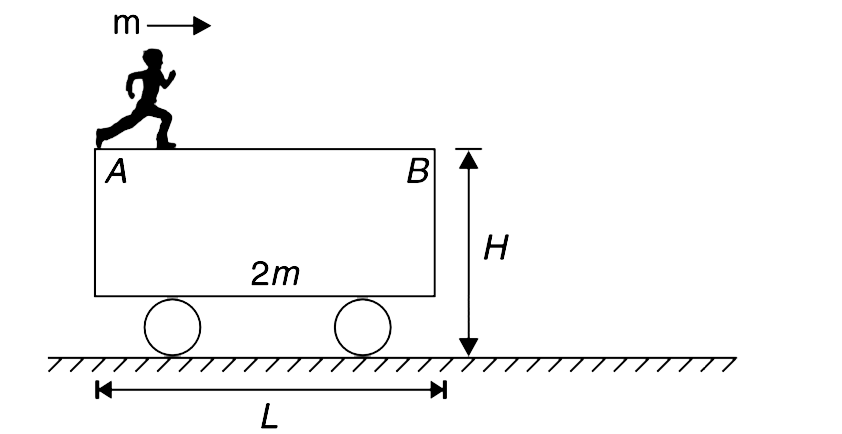
View SolutionA man of mass m is standing on the flat top of a cart of mass 2m. The length and height of the cart is LandH respectively and it is at rest on a smooth horizontal ground. The man starts running from end A, speeds up and jumps out of the cart at point B with a velocity u relative to the cart in horizontal direction. Calculate the total horizontal distance covered by the man by the time he lands on the ground.
View SolutionTwo light trollwys of masses m1 and m2(=3m1) are connected by a spring. The spring is compressed and bound by a cord. The cord is burnt through, the spring expands and the trolleys move off in opposite direction. Assume that the coefficient of friction is the same for both trollwys.
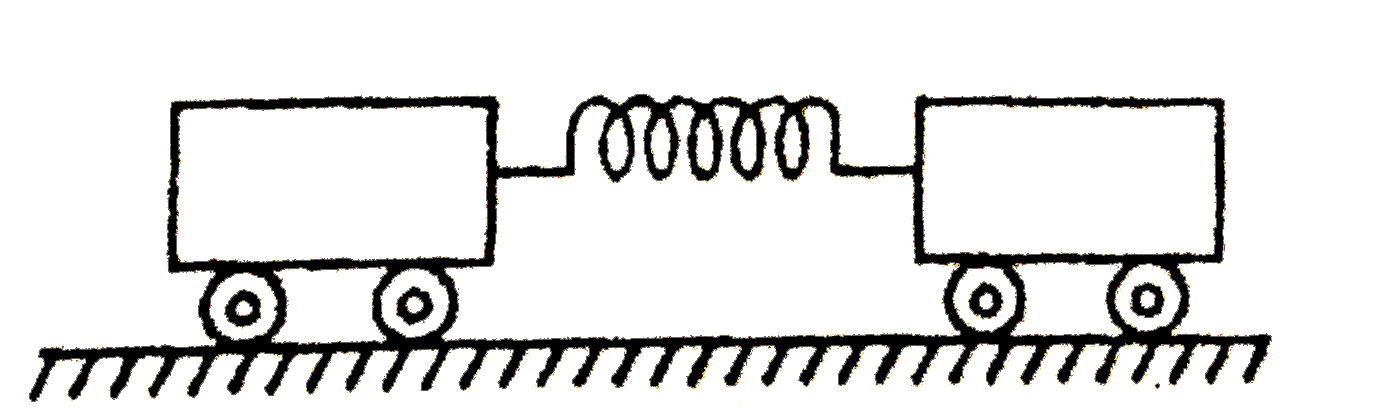
View SolutionTwo unequal masses are ties together with a cord with a compressed spring in between.
When the cord is burnt with a match releasing the spring, the two masses fly apart with equal
View SolutionA block A of mass M rests on a wedge B of mass 2M and inclination θ. There is sufficient friction between A and B so that A does not slip on B. If there is no friction between B and ground, the compression in spring is
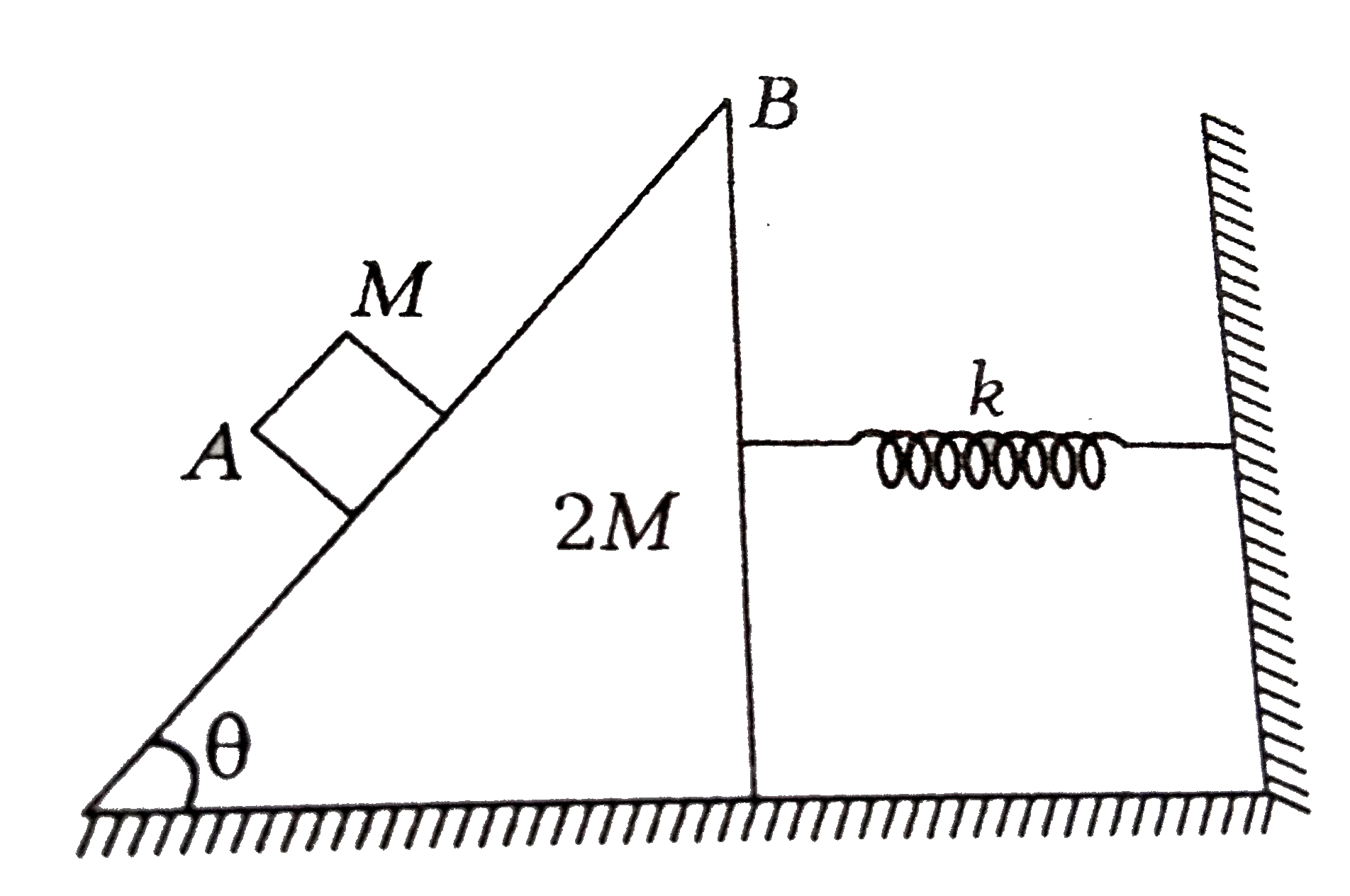
View Solution
