There is a rod of length l , its density varies with length as distance of λ=ax , where x is distance from left end. Find center of mass from left end.
Step by step video & image solution for There is a rod of length l , its density varies with length as distance of lambda=ax , where x is distance from left end. Find center of mass from left end. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
The density of a rod of length L varies as ρ=A+Bx where x is the distance from the left end. Locate the centre of mass.
 View Solution
View SolutionThe linear density of a thin rod of length 1m lies as λ=(1+2x), where x is the distance from its one end. Find the distance of its center of mass from this end.
View SolutionThe liner density of a rod of length 2m varies as λ=(2+3x) kg/m, where x is distance from end A . The distance of a center of mass from the end B will be
_PHY_E05_180_Q02.png) View Solution
View SolutionMass is non-uniformly distributed over the rod of length l, its linear mass density varies linearly with length as λ=kx2. The position of centre of mass (from lighter end) is given by-
View SolutionFind coordinates of mass center of a non-uniform rod of length L whose linear mass density lambda varies as lambda=a+bx, where x is the distance from the lighter end.
View SolutionThe centre of mass of a non-uniform rod of length L whose mass per unit length λ is proportional to x2, where x is distance from one end
View SolutionA rod of length L is of non uniform cross-section. Its mass per unit length varies linearly with distance from left end. Then its centre of mass from left end is at a distance. (Take linear density at left end=0).
 View Solution
View SolutionA thin bar of length L has a mass per unit length λ, that increases linerarly with distance from one end. If its total mass is M and its mass per unit length at the lighter end is λ0, then the distance of the centre of mass from the lighter end is
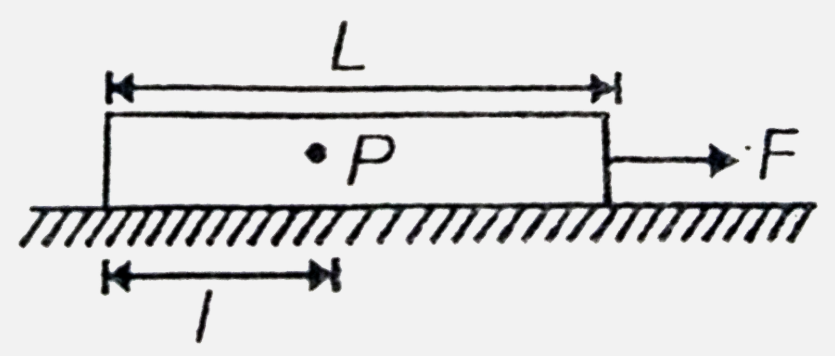
View SolutionFigure shows a rope of variable mass whose linear mass density is given by , λ=Ax , where A is + ve constant and x is distance from left end . It bis placed on a smooth horizontal surface . A force F is acting on it as shown .
(i) Find total mass of the rope .
(ii) Find tension at point P.
 View Solution
View SolutionA heavy metallic rod of non-uniform mass distribution, is hanged vertically from a rigid support. The linear mass density varies as λ(x)=k×x where x is the distance measured along the length of rod, from its lower end. Find extension in rod due to its own weight.
View Solution
