Which of the following is correct for step-up transformer? (A) Vs>Vp (B)Vs<Vp (C) Vs=Vp (D) Vs<<Vp
Step by step video & image solution for Which of the following is correct for step-up transformer? (A) V_(s)gtV_(p) (B)V_(s)ltV_(p) (C) V_(s)=V_(p) (D) V_(s)ltltV_(p) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A gas in container A is in thermal equilibrium with another gas in container B, both contain equal masses of the two gases in the respective containers. Which of the follow- ing can be true
(1) PA=PB,VA≠PBVB
(2) PAVB=PBVB
(3) PA≠PB,VA=VB
(4) PAVA=PBVBView SolutionRead the following passage and then answer questions on the basis of your under standing of the passage and the related studied concepts. Passage : For many purposes it is necessary to change an alternating voltage from one value to another value of greater/smaller magnitude. This is done with a device called transformer. A transformer consists of two sets of coils of enamelled copper wire, insulated from each other, wound on a laminated soft iron core. The primary coil has Np turns and an alternating input voltage Vp is applied to the primary coil. The secondary coil has Ns turns and produced an output voltage Vs when circuit of the secondary coil is an open circuit. For an ideal transformer, in which the primary has negligible resistance and all the flux in the core links both primary and secondary windings. For such a transformer
VsVp=NsNp=k
(a) Distinguish between a step up transformer and a step down transformer.View Solution
Knowledge Check
- Question 1 - Select One
For an ideal gas, an illustration of the different paths, A (B+C) and (D+E) from an intial state P1,V1,T1 to a final state P2,V2,T1 as shown in the given figure.

Path (A) represents a reversible isothernal expanison from P1V1 to P2V2. Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating the gas at constant volume (C) from P3,V2,T2 to P2,V2T1 to P1,V2,T3 followed by reversible cooling at a constant volume V2 (E) from P1,V2,T3 to P2,V2,T1
What is ΔS for path (D+E) ?AzeroBT2∫T1CV(T)TdTC−nRln.V2V1DnRln.V2V1 - Question 2 - Select One
When perssure is increase at constant temperature, volume of gas decreases, AB → gases,Bc → vapour +liquid ,CD → liquid critical point .At this all the physical properties of liquid phase as density of liquid = density if vapour.
Te or critical temp : Temperature above which a gas can not be liquified
Ve or critical volume : Volume occupied by one mole of gas at Te abd Pe.
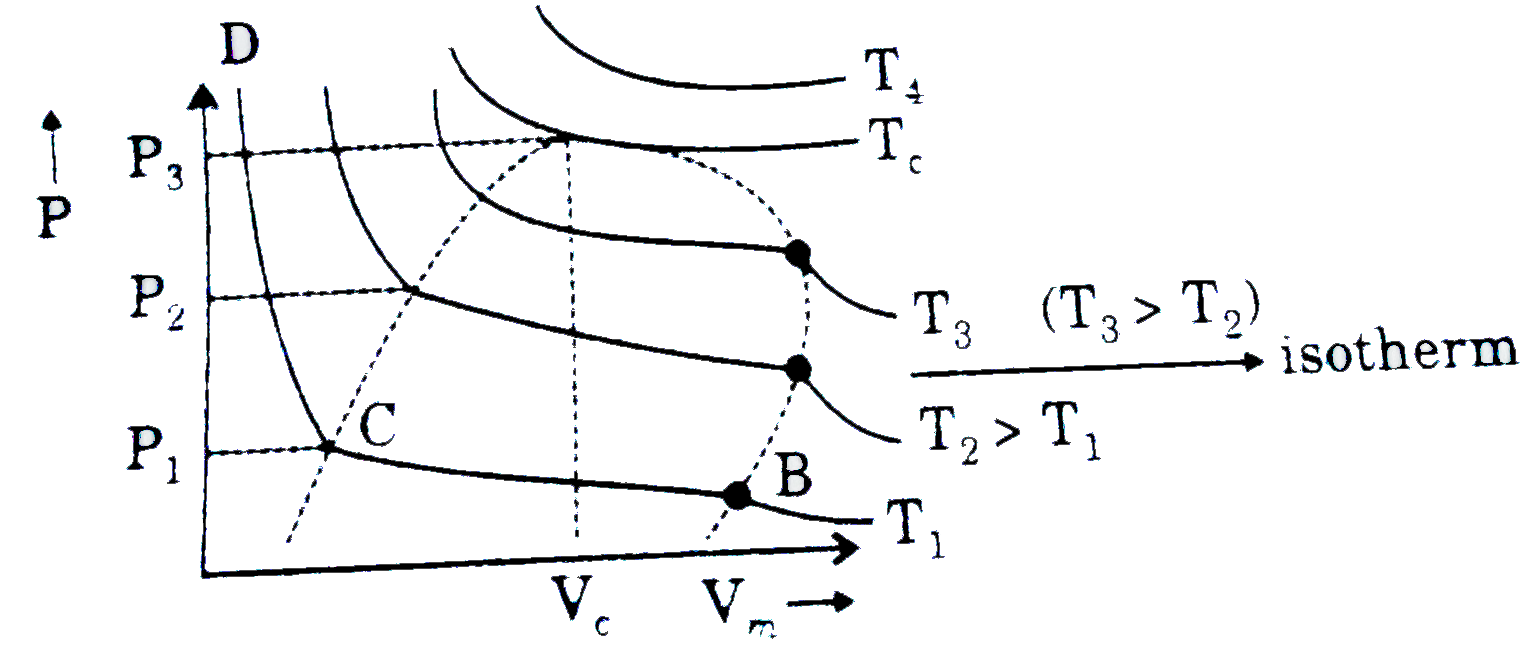
Critical constant Using van der Waals' Equations
(P+aV2m)(Vm−b)=RT
⇒(PV2m+a)(Vm−b)=RTV2m
PV3m+aVm−PbV2m=ab−RTV2m=0
⇒V3m−V2m(b+RTeP)+apVm−abp=0
Since equation is cubic in Vm hence there will be roots of equation at any temperature and pressure.At critical point van der Waals' equation will be
V3m−V2m(b+RTcPc)+apcVm−abpc=0 ....(i)
But at critical point all three roots of the equation should be equal, hence equation should be :
Vm=Vc
(Vm−Vc)3=0
Vm−3V2mVc+3VmV2c−V3c=0....(ii)
Comparing with equation (i)
b+RTcpc=3Vc ...(iii)
apc=3V2e...(iv)
abpc=V3c....(v)
from eqns.(iv) and (v0, Vc=3b
from eq. (iv) pc=a3V2c substituting pc=a3(3b)2=a27b2
from e.q (iii) RTcpc=3Vc−b=9b−b=8b
⇒Tc=8a27Rb
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slpoe will be negative zero is the maximum value of slope
(∂P∂Vm)Tc=0...(iv)
∂∂Vm(∂P∂Vm)Tc=0
[Mathematically such points are known as point of inflection (where first two derivatives becomes zero) Using the two TcPc and Vc can be calculated
A scientist proposed the following equation of state
P=RTVm−BV2m+CV2m If this equation leads to the critical behaviour then critical temperature isA8B27RCBB8RCCB23RCDnone of these - Question 3 - Select One
When perssure is increase at constant temperature, volume of gas decreases, AB → gases,Bc → vapour + liquid ,CD →liquid critical point .At this all the physical properties of liquid phase as density of liquid = density if vapour.
Te or critical temp : Temperature above which a gas can not be liquified
Ve or critical volume : Volume occupied by one mole of gas at Te abd Pe.
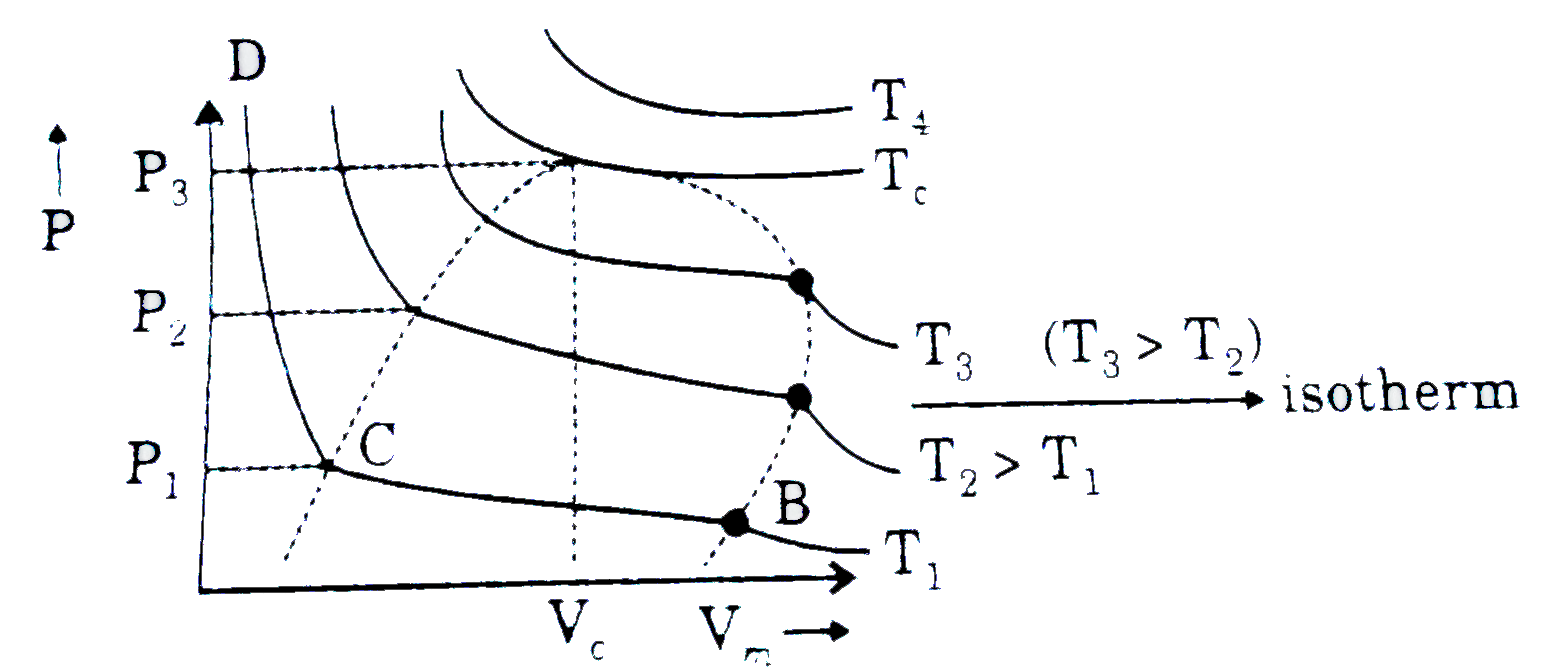
Critical constant Using van der Waals' Equations
(P+aV2m)(Vm−b)=RT
⇒(PV2m+a)(Vm−b)=RTV2m
PV3m+aVm−PbV2m=ab−RTV2m=0
⇒V3m−V2m(b+RTeP)+apVm−abp=0
Since equation is cubic in Vm hence there will be roots of equation at any temperature and pressure.At critical point van der Waals' equation will be
V3m−V2m(b+RTcPc)+apcVm−abpc=0 ....(i)
But at critical point all three roots of the equation should be equal, hence equation should be :
Vm=Vc
(Vm−Vc)3=0
Vm−3V2mVc+3VmV2c−V3c=0....(ii)
Comparing with equation (i)
b+RTcpc=3Vc ...(iii)
apc=3V2e...(iv)
abpc=V3c....(v)
from eqns.(iv) and (v0, Vc=3b
from eq. (iv) pc=a3V2c substituting pc=a3(3b)2=a27b2
from e.q (iii) RTcpc=3Vc−b=9b−b=8b
⇒Tc=8a27Rb
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slpoe will be negative zero is the maximum value of slope
(∂P∂Vm)Tc=0...(iv)
∂∂Vm(∂P∂Vm)Tc=0
[Mathematically such points are known as point of inflection (where first two derivatives becomes zero) Using the two TcPc and Vc can be calculated
If the critical constants for a hypothetical van der Waals' gas are Vc=150cm2mol−1,pc=300K Then the approxomate radius of the molecule is :
(TakeR=112Latmmol−1K−1]A(752πNA)1/3B(758πNA)1/3C(3πNA)1/3D(3256πNA)1/3
Read the following passage and then answer questions on the basis of your under standing of the passage and the related studied concepts. Passage : For many purposes it is necessary to change an alternating voltage from one value to another value of greater/smaller magnitude. This is done with a device called transformer. A transformer consists of two sets of coils of enamelled copper wire, insulated from each other, wound on a laminated soft iron core. The primary coil has Np turns and an alternating input voltage Vp is applied to the primary coil. The secondary coil has Ns turns and produced an output voltage Vs when circuit of the secondary coil is an open circuit. For an ideal transformer, in which the primary has negligible resistance and all the flux in the core links both primary and secondary windings. For such a transformer
VsVp=NsNp=k
Does working of a transformer violate the law of conservation of energy?View SolutionWhen perssure is increase at constant temperature, volume of gas decreases, AB → gases,BC → vapour +liquid ,CD → liquid critical point .At this all the physical properties of liquid phase as density of liquid = density if vapour.
Te or critical temp : Temperature above which a gas can not be liquified
Ve or critical volume : Volume occupied by one mole of gas at Te abd Pe.
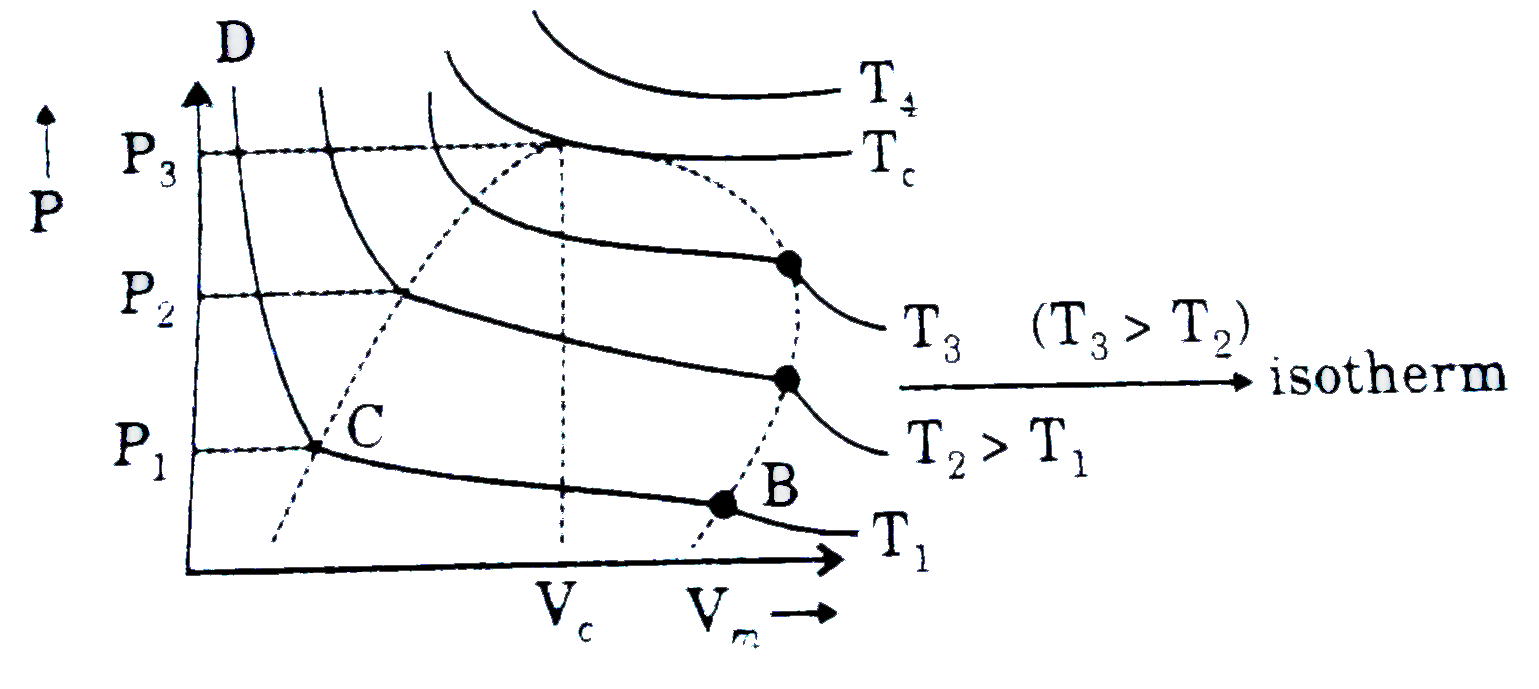
Critical constant Using van der Waals' Equations
(P+aV2m)(Vm−b)=RT
⇒(PV2m+a)(Vm−b)=RTV2m
PV3m+aVm−PbV2m=ab−RTV2m=0
⇒V3m−V2m(b+RTeP)+apVm−abp=0
Since equation is cubic in Vm hence there will be roots of equation at any temperature and pressure.At critical point van der Waals' equation will be
V3m−V2m(b+RTcPc)+apcVm−abpc=0 ....(i)
But at critical point all three roots of the equation should be equal, hence equation should be :
Vm=Vc
(Vm−Vc)3=0
Vm−3V2mVc+3VmV2c−V3c=0....(ii)
Comparing with equation (i)
b+RTcpc=3Vc ...(iii)
apc=3V2e...(iv)
abpc=V3c....(v)
from eqns.(iv) and (v0, Vc=3b
from eq. (iv) pc=a3V2c substituting pc=a3(3b)2=a27b2
from e.q (iii) RTcpc=3Vc−b=9b−b=8b
⇒Tc=8a27Rb
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slpoe will be negative zero is the maximum value of slope
(∂P∂Vm)Tc=0...(iv)
∂∂Vm(∂P∂Vm)Tc=0
[Mathematically such points are known as point of inflection (where first two derivatives becomes zero) Using the two TcPc and Vc can be calculated
Identify the wrong statement related to the following graph
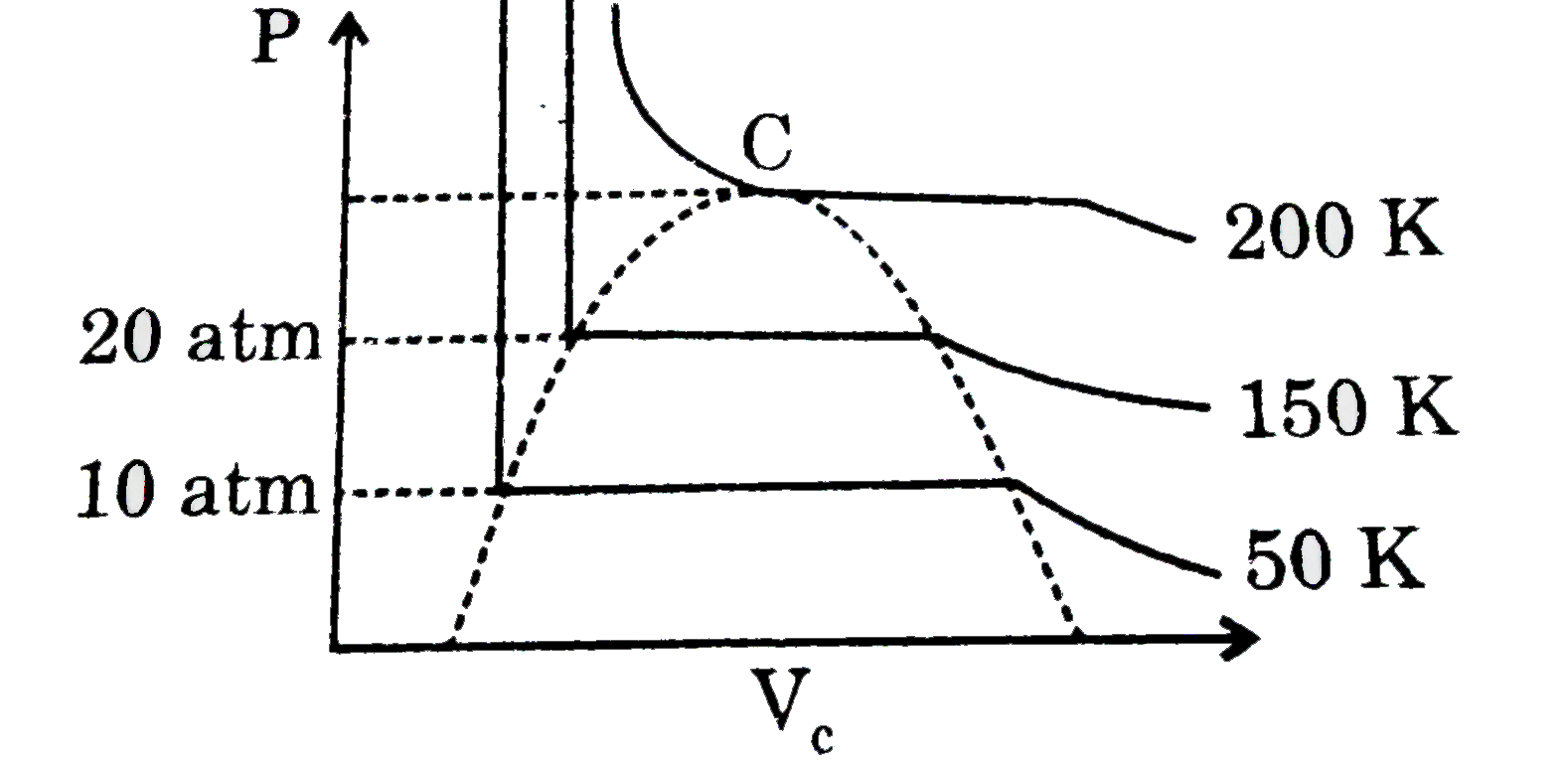 View Solution
View Solution
When pressure is increases at constant temp volume of gas decreases AB→gases,BC→vpour+liquCD→liqu
critical point: At this point all the physical propeties of liquid phase will be same as the physical properties in vapour such as, density of liquid = density of vapour
Tc or critical temp: Temperature abive which a gas can not be liquified
Pc or critical pressure: minimum pressure which must be applied at critical temp to convert the gas into liqid.
Vc or critical volume: volume occupied by one mole of gas at Tc&Pc
CRITICAL CONSTANT USING VANDERWAAL EQUATIONS:
(P+aV2m)(Vm−gb)=RT==⇒(PV2m+a)(Vm−b)=RTV2mPV3m+aVm−PbV2m−ab−RTV2m=0==⇒V3m+V2m(b+RTP)+aPVm−abP=0
since equation is cubic in Vm hence there will be three roots of equation of any temperature and pressure. At critical point all three roots will coincide and will given single value of Vm=Vc at critical point. Vander Waal equation will be
V3m−V2m(b+RTCPC)+aPCVm−abPC=0...(i)
But at critical point all three roots of the equation should be equal, hence equation should be:
Vm=Vc
(Vm−Vc)3=0
V3m−3V2mVc+3VmV2c−V3c=0..(2)
comparing with equation (1)
b+RTcPc=3Vc ...(i) aPc=3V2c ...(ii) abPc=V3c ..(iii)
From (ii) and (iii), Vc=3b
From (ii) Pc=a3V2c substituting Pc=a3(3b)2=a27b2
From (i) RTcPc=3Vc−b=9b−b=8b⇒Tc=8a27Rb
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slope will be negative zero is the maximum value of slope.
(∂P∂Vm)TC=0..(i)∂∂Vm(∂P∂Vm)TC=0...(ii)
{Mathematically such points an known as point of inflection (where first two derivatives becimes zero)}
using the two TcPc and Vc can be calculated by

If the critical constants for a hypotentical gas are Vc=150cm3mol−1.Pc=50atm and Tc=300K. then the radius of the molecule is: [Take R=112Ltratmmol−1K−1]View Solution
When pressure is increases at constant temp volume of gas decreases AB→gases,BC→vpour+liquCD→liqu
critical point: At this point all the physical propeties of liquid phase will be same as the physical properties in vapour such as, density of liquid = density of vapour
Tc or critical temp: Temperature abive which a gas can not be liquified
Pc or critical pressure: minimum pressure which must be applied at critical temp to convert the gas into liqid.
Vc or critical volume: volume occupied by one mole of gas at Tc&Pc
CRITICAL CONSTANT USING VANDERWAAL EQUATIONS:
(P+aV2m)(Vm−gb)=RT==⇒(PV2m+a)(Vm−b)=RTV2mPV3m+aVm−PbV2m−ab−RTV2m=0==⇒V3m+V2m(b+RTP)+aPVm−abP=0
since equation is cubic in Vm hence there will be three roots of equation of any temperature and pressure. At critical point all three roots will coincide and will given single value of Vm=Vc at critical point. Vander Waal equation will be
V3m−V2m(b+RTCPC)+aPCVm−abPC=0...(i)
But at critical point all three roots of the equation should be equal, hence equation should be:
Vm=Vc
(Vm−Vc)3=0
V3m−3V2mVc+3VmV2c−V3c=0..(2)
comparing with equation (1)
b+RTcPc=3Vc ...(i) aPc=3V2c ...(ii) abPc=V3c ..(iii)
From (ii) and (iii), Vc=3b
From (ii) Pc=a3V2c substituting Pc=a3(3b)2=a27b2
From (i) RTcPc=3Vc−b=9b−b=8b⇒Tc=8a27Rb
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slope will be negative zero is the maximum value of slope.
(∂P∂Vm)TC=0..(i)∂∂Vm(∂P∂Vm)TC=0...(ii)
{Mathematically such points an known as point of inflection (where first two derivatives becimes zero)}
using the two TcPc and Vc can be calculated by

A scientist proposed the following equation of state P=RTVm−BV2m+CV3m. If this equation leads to teh critical behaviour then critical temperature is:View SolutionWhich statements (s) is/are correct about osmotic pressure (P), volume (V) and temperature (T) ?
View Solution
