दोनों सिरों पर परिबद्ध क्षैतिज तनित डोरी पाँचवीं गुणावृत्ति समीकरण y(x,t)=(0.01m)sin[(62.8m−1)x]cos[(628s−1)t] द्वारा कंपित हो रही है । यदि π=3.14 माना जाय तब निम्न प्रकथन सही है/हैं
निस्पंदों की संख्या 5 है ।
डोरी की लम्बाई 0.25 m है
साम्यावस्था से डोरी के मध्यबिन्दु का अधिकतम विस्थापन 0.01 m है |
मूल आवृत्ति 100 Hz है ।
Step by step video & image solution for दोनों सिरों पर परिबद्ध क्षैतिज तनित डोरी पाँचवीं गुणावृत्ति समीकरण y(x, t) = (0.01 m) sin [(62.8 m^(-1)) x] cos [(628 s^(-1))t] द्वारा कंपित हो रही है । यदि pi= 3.14 माना जाय तब निम्न प्रकथन सही है/हैं by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE ADVANCED पेपर - 1 (2013)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 1 (2013)EXERCISE - PART I : PHYSICS (खण्ड - 3: (पूर्णांक मान सही प्रकार))
5 Videos
- JEE ADVANCED पेपर - 1 (2013)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 1 (2013)EXERCISE - PART I : PHYSICS (खण्ड - 3: (पूर्णांक मान सही प्रकार))
5 Videos
- JEE ADVANCED पेपर - 1 (2012)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 1 (2012)EXERCISE - भाग -I भौतिक विज्ञान खंड - III : पूर्णांक उत्तर प्रकार
5 Videos
- JEE ADVANCED पेपर - 1 (2014)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 1 (2014)EXERCISE - PART I : PHYSICS (खण्ड -2 : (एक पूर्णांक मान सही प्रकार) )
10 Videos
Similar Questions
एक 50 kg व 0.4m त्रिज्या की एकसमान डिस्क अपनी ऊर्ध्वाधर अक्ष के गिर्द 10rad s−1 के कोणीय वेग से घूम रही है । दो एकसमान वृत्ताकार छल्ले धीरे से डिस्क पर सममित तरीके से एक दूसरे को छूते हुए इस प्रकार डिस्क तल पर रखे जाते हैं कि वे डिस्क के अक्ष को भी स्पर्श करें । प्रत्येक छल्ले का द्रव्यमान 6.25 kg व त्रिज्या 0.2 m है । इस निकाय का नया कोणीय वेग ( rad s−1में) निम्न होगा (मान लीजिये कि डिस्क एवम् छल्ले के बीच घर्षण इतना है कि डिस्क व छल्ले के बीच सापेक्ष गति शून्य है और निकाय मूल अक्ष पर घूर्णन कर रहा है) :
View Solutionएक 50 kg व 0.4m त्रिज्या की एकसमान डिस्क अपनी ऊर्ध्वाधर अक्ष के गिर्द 10rad s−1 के कोणीय वेग से घूम रही है । दो एकसमान वृत्ताकार छल्ले धीरे से डिस्क पर सममित तरीके से एक दूसरे को छूते हुए इस प्रकार डिस्क तल पर रखे जाते हैं कि वे डिस्क के अक्ष को भी स्पर्श करें । प्रत्येक छल्ले का द्रव्यमान 6.25 kg व त्रिज्या 0.2 m है । इस निकाय का नया कोणीय वेग ( rad s−1में) निम्न होगा (मान लीजिये कि डिस्क एवम् छल्ले के बीच घर्षण इतना है कि डिस्क व छल्ले के बीच सापेक्ष गति शून्य है और निकाय मूल अक्ष पर घूर्णन कर रहा है) :
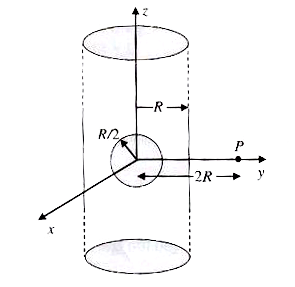
View Solutionअपरिमित लम्बाई और R त्रिज्या के एक ठोस बेलन पर एकसमान आयतन-आवेश-घनत्व ρ है। इसमें R/2 त्रिज्या का
एक खोखला गोलीय-कोष बेलन के अक्ष पर केन्द्रित है (चित्र देखिये)। अक्ष से 2R दूरी पर स्थित बिन्दु P पर वैद्युत-क्षेत्र
23ρR16kε0 से दिया जाता है । तब k का मान क्या है?
View Solutionदो समान्तर तार कागज के तल में एक दूसरे से X0 दूरी पर हैं | दोनों तारों के बीच एक बिन्दु आवेश, जो उसी तल में है तथा एक तार से X1 दूरी पर है, चाल u से गतिमान है । जब तारों में परिमाण l की विद्युत धारा एक ही दिशा में प्रवाहित की जाती है, बिन्दु आवेश के पथ की वक्रता त्रिज्या R, है । इसके विपरीत, यदि दोनों तारों में धारा I की दिशा एक दूसरे के विपरीत हो, तब पथ की वक्रता त्रिज्या R2 है । यदि X0X1=3 तब R1R2 का मान है :
View SolutionA horizontal stretched string, fixed at two ends, is vibrating in its fifth harmonic according to the equation, y(x,t)=(0.01 m) sin[(62.8 m^(-1)x] cos[(628 s^(-1))t] . Assuming p = 3.14 , the correct statement(s) is (are)
View SolutionA horizontal stretched string, fixed at two ends, is vibrating in its fifth harmonic according to the equation, y(x,t)=(0.01m)sin[(628s−1)t]. Assuming π=3.14 , the correct statement(s) is (are) :
View Solutionमाना की 2×2 सम्मिमित आव्यूह M के सभी पूर्णांक है तब M व्यत्क्रमणीय है यदि-
View Solutionयदि A=[axya] और यदि xy=1, तब det(AAT) के बराबर है
View Solutionयदि dydx=ex+y और दिया है x=1 पर y=1, तब x=−1 पर y ज्ञात कीजिए |
View Solutionयदि x=acos3θ,y=asin3θ, तब 1+(dydx)2 है-
View Solutionमाना y=y(x), अवकल समीकरण (x2+1)2dydx+2x(x2+1)y=1 का हल है, जबकि y(0) = 0 है। यदि √ay(1)=π32 है तो 'α' का मान है
View Solutionयदि 2y=(cot−1(√3cosx+sinxcosx−√3sinx))2,x∈(0,π2) तब dydx बराबर है|
View Solutionमाना y = y(x) अवकल समीकरण xdydx+y=xlogex,(x>1) का हल है । यदि 2y(2)=loge4−1 है, तो y(e) बराबर है
View Solutionयदि 3x=4x−1 तब x बराबर है
View Solutionदिया है बहुपद f(x)=1+2x+3x2+4x3.
माना कि f(x) के भिन्न, वास्तविक मूलो का योग S है तथा t=|S| है |
Q. वास्तविक संख्या S, निम्न अन्तराल में है
View Solutionयदि sinx+siny=3(cosy−cosx), तब sin3xsin3y का मान है
View Solution
