A block at rest slides down a smooth inclined plane which makes an angle 60∘ with the vertical and it reaches the ground in t1 seconds. Another block is dropped vertically from the same point and reaches the ground in t2 seconds. Then the ratio of t1:t2 is
1:2
2:1
1:3
1:√2
The correct Answer is:B
To solve the problem, we need to analyze the motion of both blocks: one sliding down the inclined plane and the other dropped vertically.
1. Understanding the Setup:
- We have two blocks:
- Block A slides down a smooth inclined plane making an angle of 60∘ with the vertical.
- Block B is dropped vertically from the same height H.
- We need to find the ratio of the time taken by Block A to reach the ground (t1) to the time taken by Block B (t2).
2. Finding the Time for Block B:
- For Block B, which is dropped vertically, we can use the second equation of motion:
H=12gt22
- Rearranging gives:
t22=2Hg
3. Finding the Time for Block A:
- For Block A, we need to analyze the forces acting on it. The component of gravitational force acting down the incline is mgsin(60∘).
- The acceleration a of Block A along the incline is:
a=gsin(60∘)=g⋅√32
- The distance traveled along the incline can be related to the height H using the relationship:
H=Lcos(60∘)⇒L=Hcos(60∘)=2H
- Now, applying the second equation of motion for Block A:
L=12at21
- Substituting L and a:
2H=12(g⋅√32)t21
- Rearranging gives:
t21=4Hg⋅√32=8Hg√3
4. Finding the Ratio t1:t2:
- We have:
t22=2Hgandt21=8Hg√3
- Taking the ratio:
t21t22=8Hg√32Hg=82√3=4√3
- Therefore:
t1t2=√4√3=2√(4)3=2√33
5. Final Ratio:
- The ratio t1:t2 simplifies to:
t1:t2=2:1
Final Answer:
The ratio of t1:t2 is 2:1.
- We have two blocks:
- Block A slides down a smooth inclined plane making an angle of 60∘ with the vertical.
- Block B is dropped vertically from the same height H.
- We need to find the ratio of the time taken by Block A to reach the ground (t1) to the time taken by Block B (t2).
- For Block B, which is dropped vertically, we can use the second equation of motion:
H=12gt22
- Rearranging gives:
t22=2Hg
- For Block A, we need to analyze the forces acting on it. The component of gravitational force acting down the incline is mgsin(60∘).
- The acceleration a of Block A along the incline is:
a=gsin(60∘)=g⋅√32
- The distance traveled along the incline can be related to the height H using the relationship:
H=Lcos(60∘)⇒L=Hcos(60∘)=2H
- Now, applying the second equation of motion for Block A:
L=12at21
- Substituting L and a:
2H=12(g⋅√32)t21
- Rearranging gives:
t21=4Hg⋅√32=8Hg√3
- We have:
t22=2Hgandt21=8Hg√3
- Taking the ratio:
t21t22=8Hg√32Hg=82√3=4√3
- Therefore:
t1t2=√4√3=2√(4)3=2√33
- The ratio t1:t2 simplifies to:
t1:t2=2:1
The ratio of t1:t2 is 2:1.
Topper's Solved these Questions
- FRICTION BOOK - ERRORLESSCHAPTER - FRICTION EXERCISE - PAST YEARS QUESTIONS
11 Videos
- FRICTION BOOK - ERRORLESSCHAPTER - FRICTION EXERCISE - ASSERTION & REASON
8 Videos
- FRICTION BOOK - ERRORLESSCHAPTER - FRICTION EXERCISE - NCERT BASED QUESTIONS (Kinetic Friction )
20 Videos
- FLUID MECHANICSBOOK - ERRORLESSCHAPTER - FLUID MECHANICSEXERCISE - ASSERTION AND REASON
23 Videos
- GRAVITATIONBOOK - ERRORLESSCHAPTER - GRAVITATIONEXERCISE - Assertion and Reason
25 Videos
Similar Questions
A body projected vertically upwords from the top of a tower reaches the ground in t1 second . If it projected vertically downwards from the some top with same velocity ,it reaches the ground in t2seconds . If it is just dropped from the top it reaches the ground in t second .prove that t=√t1t2
View SolutionFrom the top of a tower, a stone is thrown up. It reaches the ground in 5 sec. A second stone is thrown down with the same speed and reaches the ground in 1 sec. A third stone is released from rest and reaches the ground in
View Solution
Knowledge Check
A block slides down a smooth inclined plane when released from the top, while another falls freely from the same point :
Asliding block will reach the ground first with greater speedBfreely falling block will reach the ground first with greater speedCboth the blocks will reach the ground at the same time but with different speedsDboth the blocks will reach the ground with same speed but the freely falling block firstFrom the top of a tower, a stone is thrown up and it reaches the ground in time t1A second stone is thrown down with the same speed and it reaches the ground in time t2 A third stone is released from rest and it reaches the ground in time The correct relation between t1,t2 and t3 is :
At3=12(t1+t2)Bts=√t1t2C1t3=1t2−1t1Dt2t3=23−t22A block released from rest from the tope of a smooth inclined plane of angle of inclination θ1=30∘ reaches the bottom in time t1. The same block, released from rest from the top of another smooth inclined plane of angle of inclination θ2=45∘ reaches the bottom in time t2. Time t1 and t2 are related as ( Assume that the initial heights of blocks in the two cases are equal ).
At2t1=1√2Bt2t1=12Ct2t1=1Dt1t2=12
A body projected vertically upwards from A, the top of a tower, reaches the ground in t1 seconds.If it is projected vertically downwards from A with the same velocity, it reaches the ground in t2 seconds.If it falls freely from rest at A, in what time does it reach the ground ?
View SolutionA ball proected vetically upwards from (A), the top fo tower reaches the ground in t1 second. If it is projected vectically downwards from (A) with the same vecoty, it reaches the ground in t2secons.Ifitfallseelyom(A),showtˆitwod––reahctheground∈ sqrt t_1 t-2 seconds.
View SolutionA balloon starts rising upwards with constant acceleration a and afrer time t0, second, a packet is dropped from it which reaches the ground aftre t seconds of dropping . Derermine the value of t
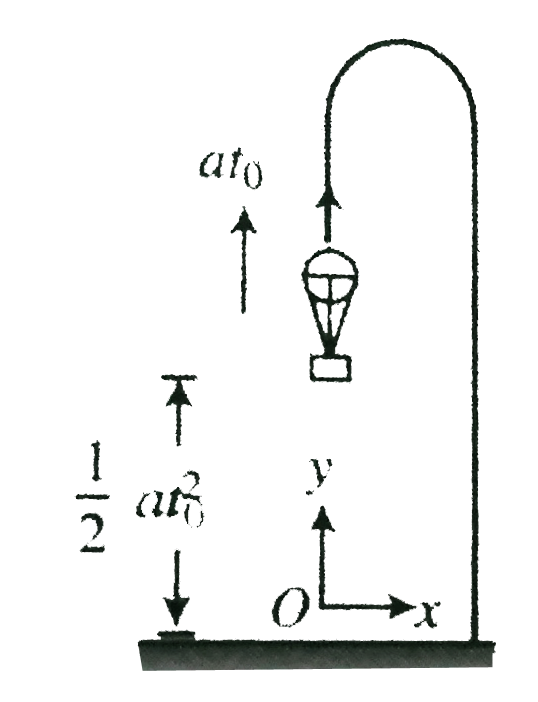 .
.
View SolutionA block released from rest from the top of a smooth inclined plane of angle θ1 reaches the bottom in t1 .
The same block relased from rest from the top of another smooth inclined plane of angle θ2 , reaches the bottom in time t2 . If the two inclined planes have the same height, the relation between t1andt2 is
View SolutionFrom the top of a tower a stone is thrown up which reaches the ground in time t1. A second stone thrown down with the same speed reaches the ground in a time t2. A third stone released from rest from the same location reaches the ground in a time t3. then:
View Solution
