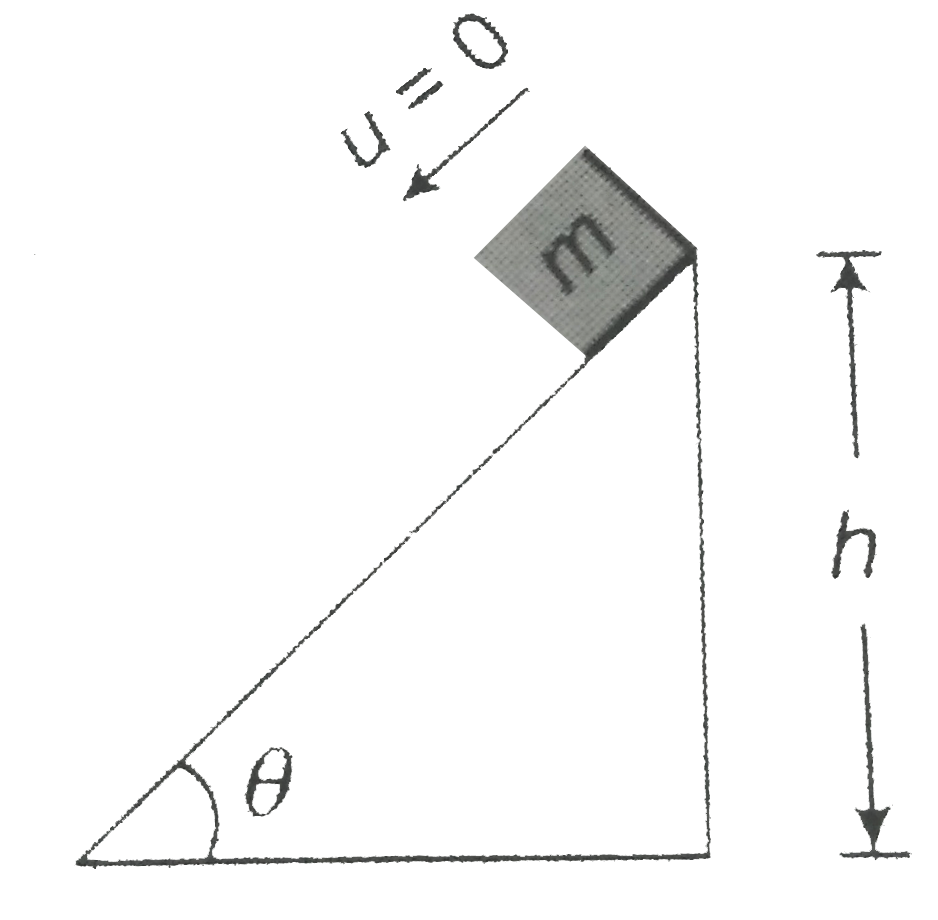
A block is kept on an inclined plane of inclination $θ$ of length l. the velocity of particle at the bottom of inclined is (the coefficient of friciton is $μ$ )

A

$\sqrt{2 g l (μ cos θ - sin θ)}$

B

$\sqrt{2 g l (sin θ - μ cos θ)}$

C

$\sqrt{2 g (sin θ + μ cos θ)}$

D

$\sqrt{2 g (cos θ + μ sin θ)}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$a = g (sin θ - μ cos θ), s = 1$
$v^{2} = u^{2} + 2 a s,$ u = 0
$\Rightarrow v = \sqrt{2 a s} = \sqrt{2 g l (sin θ - μ cos θ)}$

|

Updated on:21/07/2023

Class 11 PHYSICS FRICTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
An object is placed on the surface of a smooth inclined plane of inclination $θ$ . It takes time t to reach the bottom. If the same object is allowed to slide down a rough inclined plane of inclination $θ$ , it takes time nt to reach the bottom where n is a number greater than 1. The coefficient of friction $μ$ is given by:-
A $μ = tan θ (1 - \frac{1}{n^{2}})$
B $μ = cot θ (1 - \frac{1}{n^{2}})$
C $μ = tan θ \sqrt{1 - \frac{1}{n^{2}}}$
D $μ = cot θ \sqrt{1 - \frac{1}{n^{2}}}$
Question 2 - Select One
A block is released from the top of an inclined plane of inclination $θ$ . Its velocity at the bottom of plane is $v$ . If it slides down a rough inclined plane of the same inclination , its velocity at bottom is $v / 2$ . The coefficient of friction is
A $\frac{3}{4} cos θ$
B $\frac{1}{4} cos θ$
C $\frac{1}{4} tan θ$
D $\frac{3}{4} tan θ$
Question 3 - Select One
A block moves down a smooth inclined plane of inclination $θ$ . Its velocity on reaching the bottom is v. If it slides down a rough inclined plane of some inclination, its velocity on reaching the bottom is v/n, where n is a number greater than 0. The coefficient of friction is given by -
A $μ = tan θ (1 - \frac{1}{n^{2}})$
B $μ = cot θ (1 - \frac{1}{n^{2}})$
C $μ = tan θ (1 + \frac{1}{n^{2}})$
D $μ = cot θ (1 + \frac{1}{n^{2}})$

ERRORLESS-FRICTION -NCERT BASED QUESTIONS (Motion on Inclined Surface )

Home
Ask Doubt
Profile