If the ratio of diameters, lengths and Young’s modulus of steel and copper wires shown in the figure are p, q and s respectively, then the corresponding ratio of increase in their lengths would be

5q(7sp2)
7q(5sp2)
2q(5sp)
7q(5sp)
The correct Answer is:B
Δl=FlAY=Flπ(d2)2Y
Δl1Δl2=(l1l2)(d2d1)2(Y2Y1)(F1F2)
=75×(q)(1p)2(1s)=7q5sp2
Topper's Solved these Questions
- BOOK - ERRORLESSCHAPTER - ELASTICITYEXERCISE - ASSERTION & REASON10videos
ELASTICITY
- BOOK - ERRORLESSCHAPTER - ELASTICITYEXERCISE - NCERT BASED QUESTIONS (Modulus of Rigidity)16videos
ELASTICITY
- BOOK - ERRORLESSCHAPTER - BASIC MATHEMATICS AND VECTORSEXERCISE - Assertion & Reason15videos
BASIC MATHEMATICS AND VECTORS
- BOOK - ERRORLESSCHAPTER - FLUID MECHANICSEXERCISE - ASSERTION AND REASON23videos
FLUID MECHANICS
Similar Questions
If the ratio of diameter, lengths and Young's modulus of steel and brass wires shown in figure are 2 : 1, 2 : 1 and 2 : 1 respectively, then the corresponding ratio of increase in their lengths would be
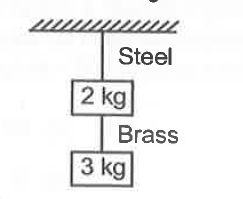 View Solution
View SolutionIf the ratio of lengths, radii and young's modulii of steel and brass wires in the figure are a,b and c, respectively. Then, the corresponding ratio of increase in their lengths would be
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If the ratio of diameters,lengths and Young's moduli of steel and brass wires shown in the figure are p, q and r respectively . Then the corresponding ratio of increase in their lenghts would be
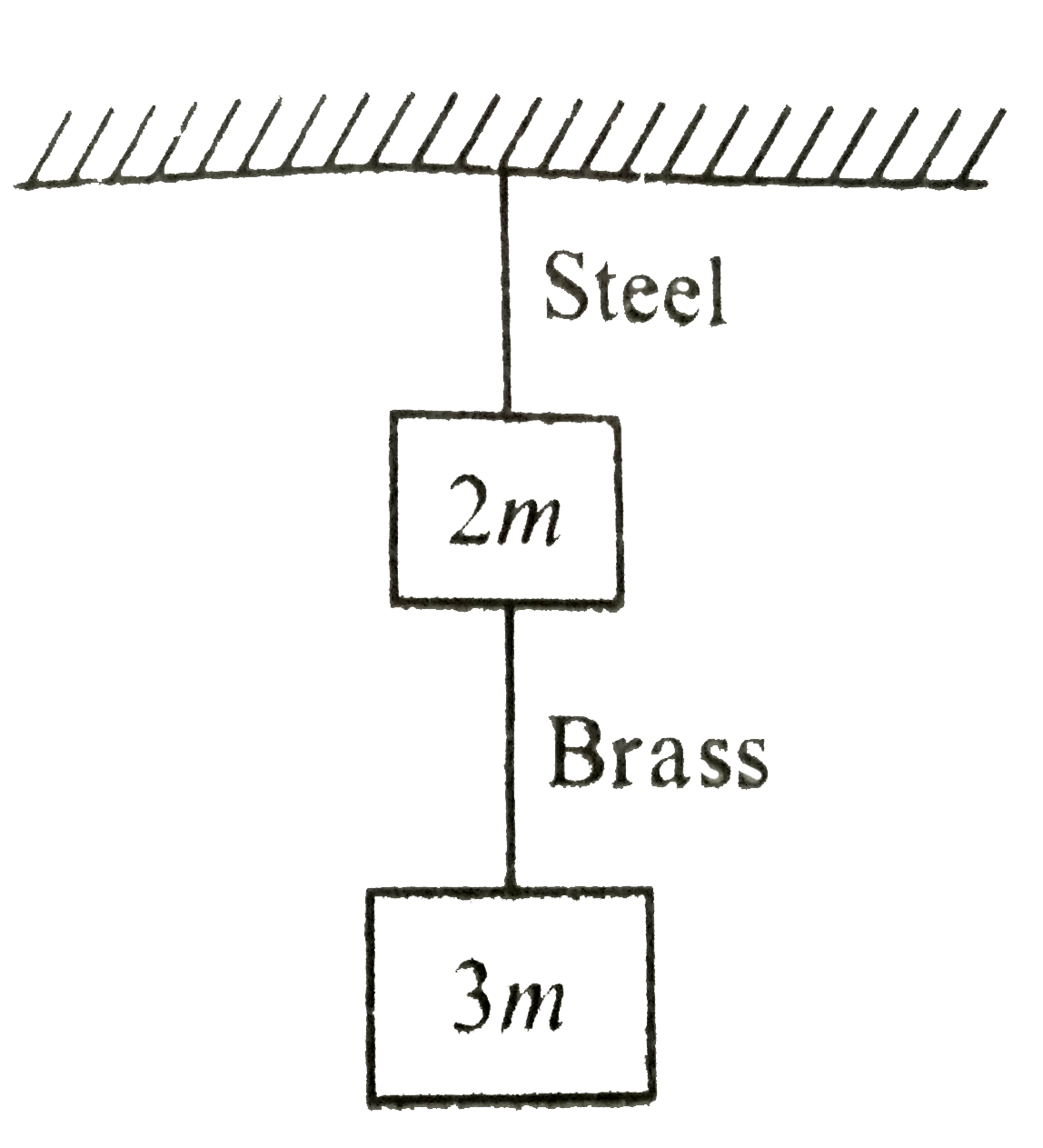 A3q5p2rB5q3p2rC3q5prD5q3pr
A3q5p2rB5q3p2rC3q5prD5q3pr - Question 2 - Select One
If the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are a,b and c respectively then the corresponding ratio of increase in their lengths is
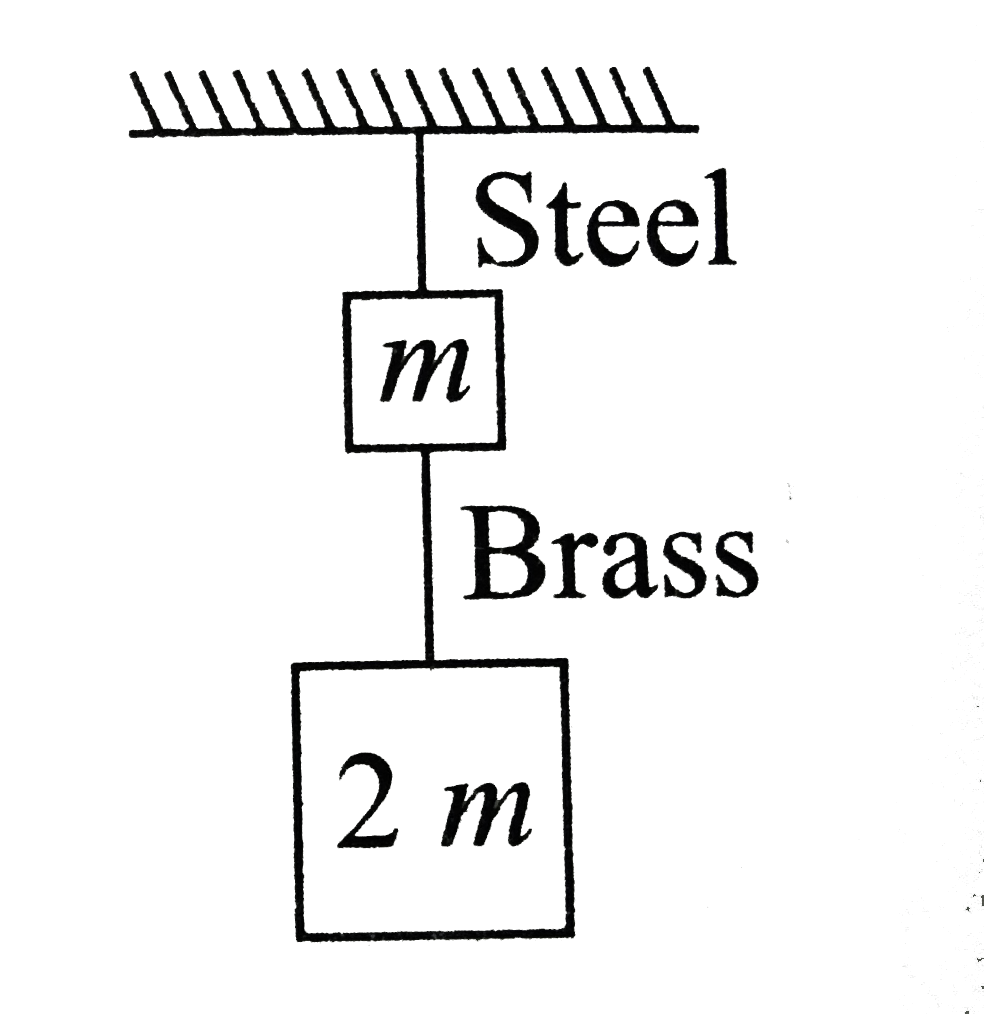 A2a2cbB3a2b2cC2acb2D3c2ab2
A2a2cbB3a2b2cC2acb2D3c2ab2 - Question 3 - Select One
If the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are a,b and c repectively then the corresponding ratio of increase in their lengths is
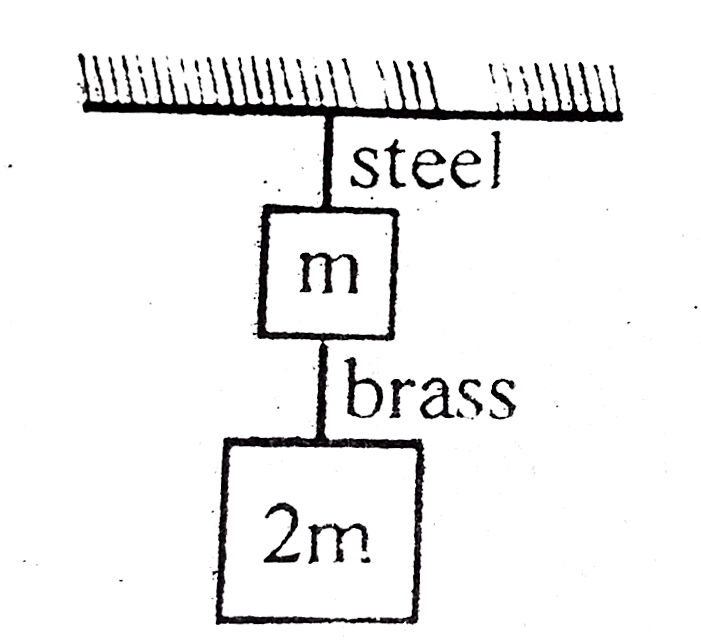 A2a2c/bB3a/2b2cC2ac/b2D3c/2ab2
A2a2c/bB3a/2b2cC2ac/b2D3c/2ab2
If the ratio of lengths, radii and youngs's modulus of steel and and brass wires in figure are 2:1,2:1,3:1 respectively. Then corresponding ratio of increases in their would be. (Neglect the mass of the wire and take g=10m/s2)
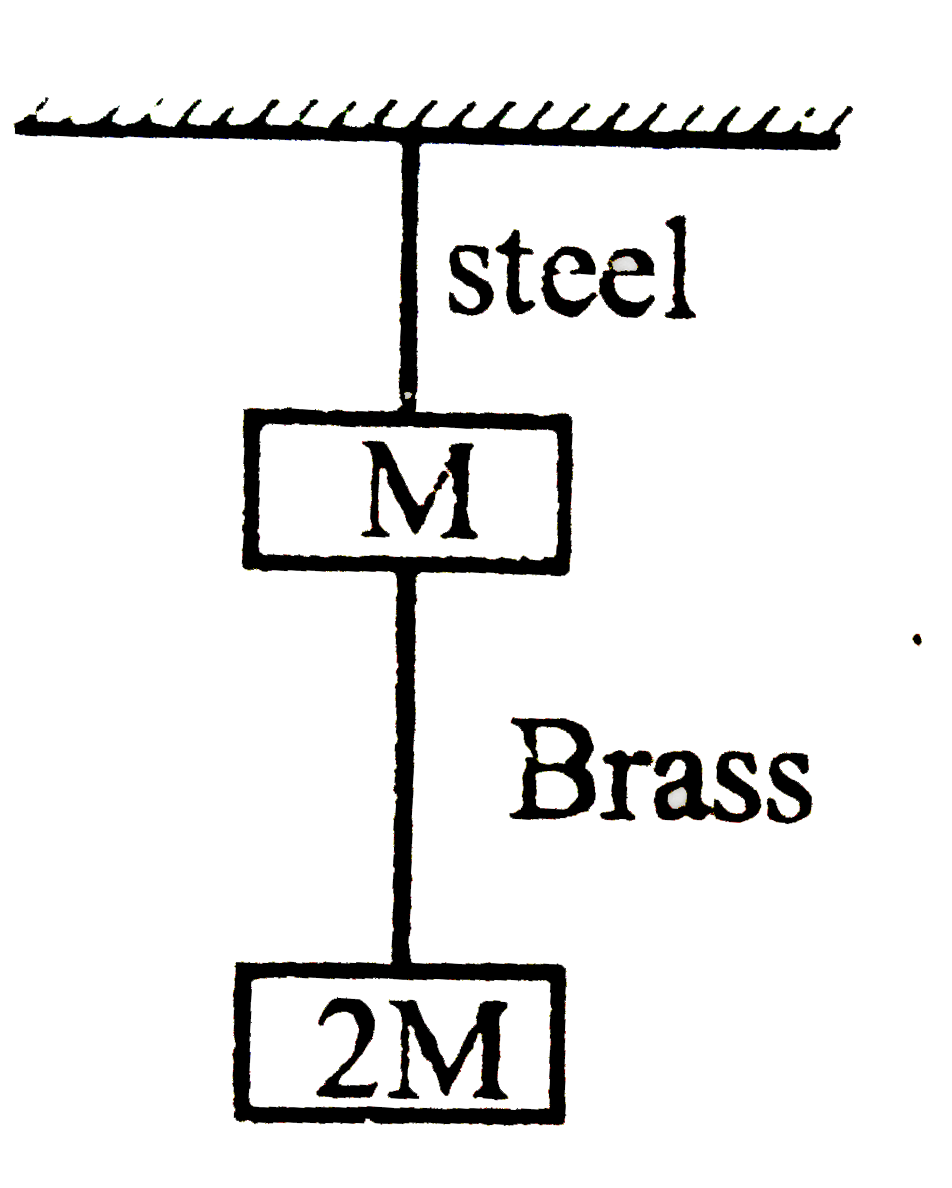 View Solution
View SolutionIf the ratio of lenghts, radi and Young's moduli of steel and brass wires are a,b and c respectively their respective loads are in the ratio 3:2 then the corresponding ratio of increases in their lenghts would be
View Solution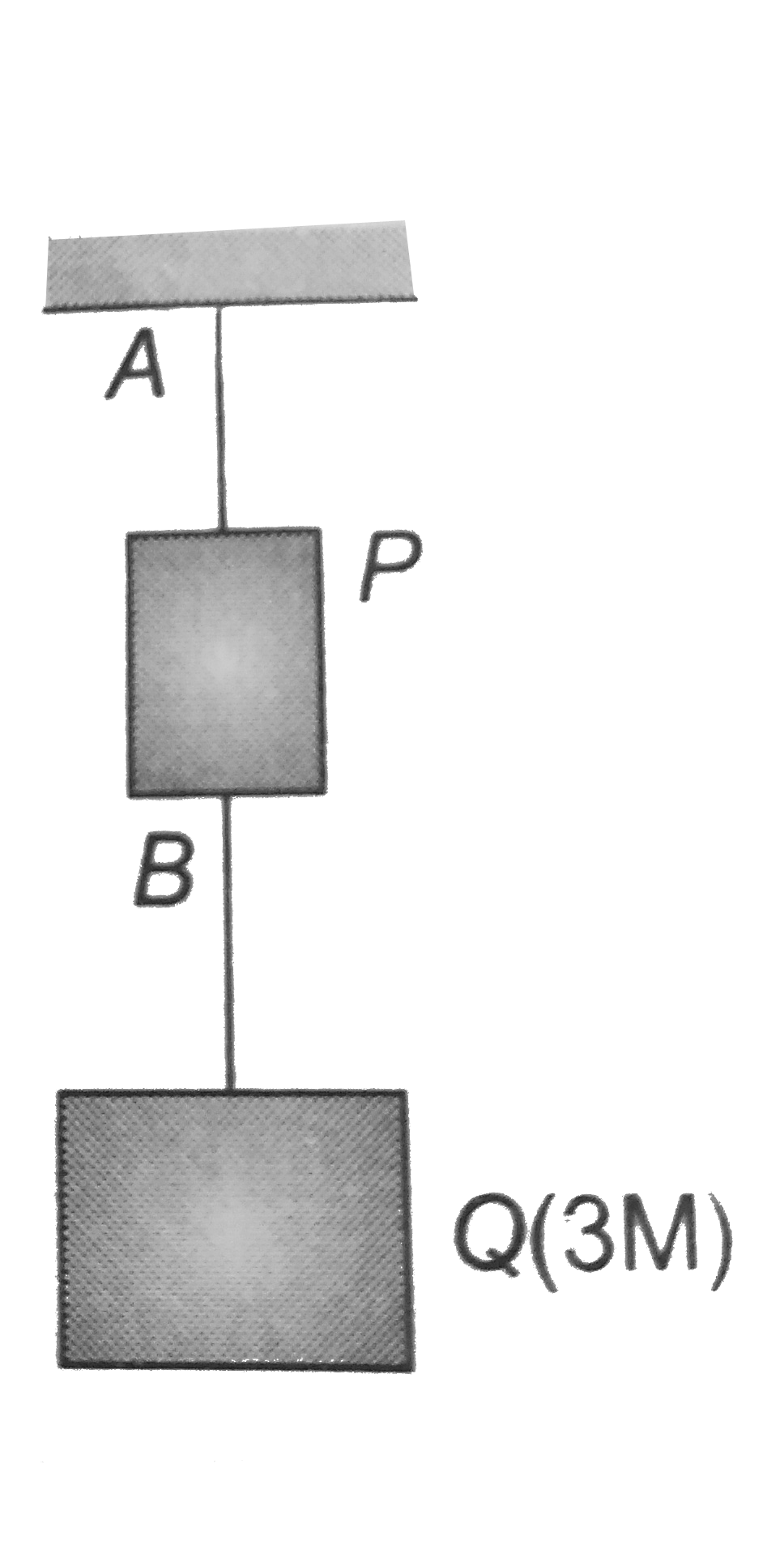
Wires A and B are connected with blocks P and Q, as shown, the ratio of lengths radii and Young's modulus of wires A and B are r, 2r and 3r respectively (r is a constant). Find the mass of block P if ratio of increase in their corresponding length is 16r2. The mass of the block Q is 3MView SolutionThe ratio of the lengths of two wires A and B of same material is 1:2 and the ratio of their diameters is 2:1. They are stretched by the same force, then the ratio of increase in length will be
View SolutionThe ratio of the lengths of two wires A and B of same material is 1:2 and the ratio of their diameter is 2:1. They are stretched by the same force, then the ratio of increase in length will be
View Solution

