A cord is wound over the rim of a flywheel of mass 20 kg and radius 25 cm. A mass 2.5 kg attached to the cord is allowed to fall under gravity. Calculate the angular acceleration of the flywheel
25rad/s2
20rad/s2
10rad/s2
5rad/s2
The correct Answer is:C
To solve the problem of finding the angular acceleration of the flywheel, we can follow these steps:
Step 1: Identify the forces acting on the falling mass
The mass m=2.5kg is falling under the influence of gravity. The force acting on it due to gravity is given by:
Fg=m⋅g
where g=9.81m/s2.
Step 2: Calculate the gravitational force
Substituting the values:
Fg=2.5kg⋅9.81m/s2=24.525N
Step 3: Write the equation of motion for the falling mass
The net force acting on the mass when it is falling can be expressed as:
Fnet=Fg−T
where T is the tension in the cord. According to Newton's second law:
Fnet=m⋅a
Thus, we have:
m⋅a=Fg−T
Step 4: Relate linear acceleration to angular acceleration
The linear acceleration a of the falling mass is related to the angular acceleration α of the flywheel by the equation:
a=r⋅α
where r=0.25m (the radius of the flywheel).
Step 5: Write the torque equation for the flywheel
The torque τ acting on the flywheel due to the tension in the cord is given by:
τ=T⋅r
According to Newton's second law for rotation:
τ=I⋅α
where I is the moment of inertia of the flywheel. For a solid disk, the moment of inertia is given by:
I=12Mr2
where M=20kg is the mass of the flywheel.
Step 6: Calculate the moment of inertia
Substituting the values:
I=12⋅20kg⋅(0.25m)2=12⋅20⋅0.0625=0.625kg⋅m2
Step 7: Substitute the torque equation
Now we can substitute the torque equation:
T⋅r=I⋅α
Substituting for I:
T⋅0.25=0.625⋅α
Step 8: Solve for tension T
From the equation of motion for the falling mass:
2.5⋅a=24.525−T
Substituting a=r⋅α=0.25⋅α:
2.5⋅(0.25⋅α)=24.525−T
This simplifies to:
0.625α=24.525−T
Thus, we can express T as:
T=24.525−0.625α
Step 9: Substitute T back into the torque equation
Substituting this expression for T into the torque equation:
(24.525−0.625α)⋅0.25=0.625⋅α
Step 10: Solve for angular acceleration α
Expanding and rearranging gives:
6.13125−0.15625α=0.625α
Combining terms:
6.13125=0.625α+0.15625α
6.13125=0.78125α
Finally, solving for α:
α=6.131250.78125≈7.85rad/s2
Final Answer:
The angular acceleration of the flywheel is approximately 7.85rad/s2.
---
The mass m=2.5kg is falling under the influence of gravity. The force acting on it due to gravity is given by:
Fg=m⋅g
where g=9.81m/s2.
Substituting the values:
Fg=2.5kg⋅9.81m/s2=24.525N
The net force acting on the mass when it is falling can be expressed as:
Fnet=Fg−T
where T is the tension in the cord. According to Newton's second law:
Fnet=m⋅a
Thus, we have:
m⋅a=Fg−T
The linear acceleration a of the falling mass is related to the angular acceleration α of the flywheel by the equation:
a=r⋅α
where r=0.25m (the radius of the flywheel).
The torque τ acting on the flywheel due to the tension in the cord is given by:
τ=T⋅r
According to Newton's second law for rotation:
τ=I⋅α
where I is the moment of inertia of the flywheel. For a solid disk, the moment of inertia is given by:
I=12Mr2
where M=20kg is the mass of the flywheel.
Substituting the values:
I=12⋅20kg⋅(0.25m)2=12⋅20⋅0.0625=0.625kg⋅m2
Now we can substitute the torque equation:
T⋅r=I⋅α
Substituting for I:
T⋅0.25=0.625⋅α
From the equation of motion for the falling mass:
2.5⋅a=24.525−T
Substituting a=r⋅α=0.25⋅α:
2.5⋅(0.25⋅α)=24.525−T
This simplifies to:
0.625α=24.525−T
Thus, we can express T as:
T=24.525−0.625α
Substituting this expression for T into the torque equation:
(24.525−0.625α)⋅0.25=0.625⋅α
Expanding and rearranging gives:
6.13125−0.15625α=0.625α
Combining terms:
6.13125=0.625α+0.15625α
6.13125=0.78125α
Finally, solving for α:
α=6.131250.78125≈7.85rad/s2
The angular acceleration of the flywheel is approximately 7.85rad/s2.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - Assertion & Reason
25 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - ASSERTION AND REASON
25 Videos
- NEWTON'S LAWS OF MOTIONBOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion & Reason
15 Videos
Similar Questions
A cord of negligible mass is wound round the rim of a flywheel of mass 20kg and radius 20cm. A steady pull of 25N is applied on the cord as shown in Fig. The flywheel is mounted on a horizontal axle with frictionless bearings.
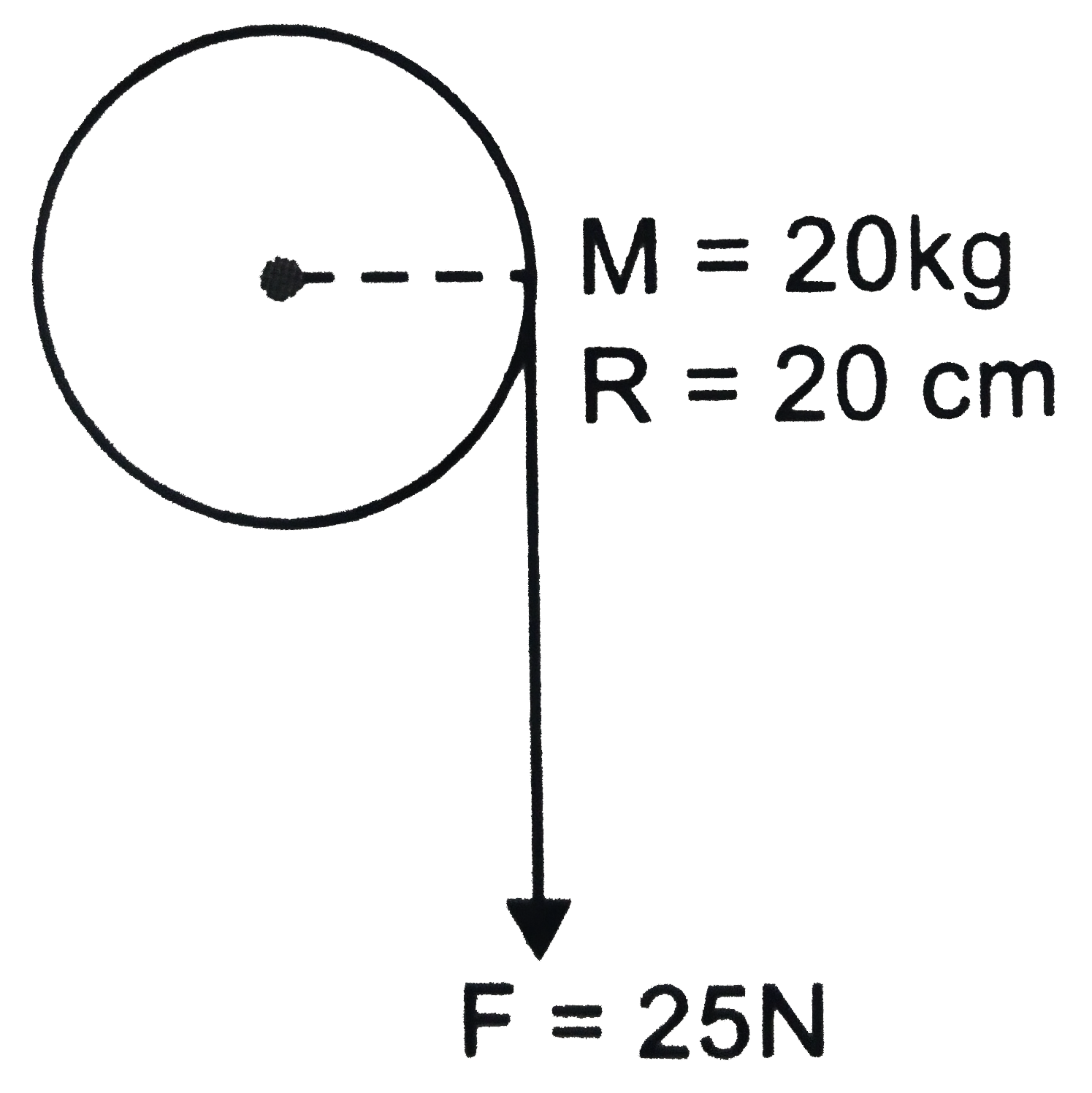
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel stars from rest.
(d) Compare answers to parts (b)and (c).
View SolutionA cord is wound around the circumference of a wheel of diameter 0.3 m. The axis of the wheel is horizontal. A mass of 0.5 kg is attached at the end of the cord and it is allowed to fall from rest. If the weight falls 1.5 m in 4s, what is the angular acceleration of the wheel ? Also find out the moment of inertia of the wheel.
View Solution
Knowledge Check
A cord is wound over the rim of a flywheel of mass 20 kg and radius 25 cm. A mass 2.5 kg attached to the cord is allowed to fall under gravity. The angular acceleration of the flywheel is
A25rad/s2B20rad/s2C10rad/s2D5rad/s2The M.I. of a wheel of mass 8 kg and radius of gyration 25 cm is
A5kgm2B1.5kgm2C2.5kgm2D0.5kgm2A string is wound round the rim of a mounted flywheel of mass 20kg and radius 20cm. A steady pull of 25N is applied on the cord. Neglecting friction and mass of the string, the angular acceleration of the wheel in rad/s2 is
A50B25C12.5D6.25
A cord of negligible mass is wound around the rim of a wheel of radius 20 cm. An object of mass 600 g is attached to the end of the cord and is allowed to fall from rest. It took 5 s for the object to fall by 2 m. Calculate the angular acceleration and moment of inertia of the wheel. Assume that the axis of wheel is horizontal.
View SolutionA body of mass 2 kg is attached to a weightless string wound round a cylinder of mass 5 kg and radius 50 cm. the body is allowed to fall. Calculate (i) tension in the string (ii) acceleration with which the body falls.
View SolutionA string is wound round the rim of a mounted flywheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord. Neglecting friction and mass of the string, the angular acceleration of the wheel is
View SolutionA cord of negligible mass is wound round the rin of a flywheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord. The work done by the pull when 2 m of the cord is unwound is
View SolutionIf a flywheel of mass m kg and radius r m is revolving at n rps, then the kinetic energy of rotation will be
View Solution
